题目内容
12．下列函数中，在其定义域内既是偶函数又在（-∞，0）上单调递增的函数是（ ）| A． | f（x）=x2 | B． | f（x）=2|x| | C． | f（x）=log2$\frac{1}{|x|}$ | D． | f（x）=sinx |
分析 根据函数奇偶性和单调性的定义和性质分别进行判断即可．
解答 解：A．f（x）=x2是偶函数，在（-∞，0）上单调递减，不满足条件．
B．f（x）=2|x|是偶函数，在（-∞，0）上单调递减，不满足条件．
C．f（x）=-log2$\frac{1}{|x|}$是偶函数，在（-∞，0）上单调递增，满足条件．
D．f（x）=sinx是奇函数，不满足条件．
故选：C．
点评 本题主要考查函数奇偶性和单调性的判断，比较基础．
练习册系列答案
相关题目
20．已知随机变量服从二项分布B（n，p），若E（x）=30，D（x）=20，则p=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{9}$ |
7．在等比数列{an}中，a3=4a1，则公比q的值为（ ）
| A． | 1 | B． | 2 | C． | 4 | D． | 8 |
17．若 ξ～B（10，$\frac{1}{4}$），则D（ξ）等于（ ）
| A． | $\frac{15}{8}$ | B． | $\frac{15}{4}$ | C． | $\frac{5}{2}$ | D． | 5 |
4．
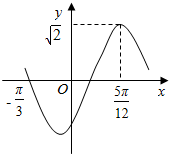函数f（x）=$\sqrt{2}$sin（ωx+θ）（x∈R，ω＞0，|θ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的单调递减区间为（ ）
函数f（x）=$\sqrt{2}$sin（ωx+θ）（x∈R，ω＞0，|θ|＜$\frac{π}{2}$）的部分图象如图所示，则f（x）的单调递减区间为（ ）| A． | $[\frac{5π}{12}+kπ，\frac{11π}{12}+kπ]，k∈z$ | B． | $[\frac{5π}{6}+kπ≤x≤\frac{11π}{6}+kπ]，k∈z$ | ||
| C． | $[\frac{5π}{12}+2kπ，\frac{11π}{12}+2kπ]，k∈z$ | D． | $[-\frac{π}{12}+kπ，\frac{5π}{12}+kπ]，k∈z$ |
1．函数f（x）=lnx+ex（e为自然对数的底数）的零点所在的区间是（ ）
| A． | $（{0，\frac{1}{e}}）$ | B． | $（{\frac{1}{e}，1}）$ | C． | （1，e） | D． | （e，+∞） |