题目内容
20.已知随机变量服从二项分布B(n,p),若E(x)=30,D(x)=20,则p=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{9}$ |
分析 直接利用二项分布的期望与方差列出方程求解即可.
解答 解:随机变量X服从二项分布B(n,p),若E(X)=30,D(X)=20,
可得np=30,npq=20,
∴q=$\frac{2}{3}$,p=$\frac{1}{3}$,
故选:B.
点评 本题考查离散型随机变量的分布列的期望以及方差的求法,考查计算能力.

练习册系列答案
相关题目
12.下列函数中,在其定义域内既是偶函数又在(-∞,0)上单调递增的函数是( )
| A. | f(x)=x2 | B. | f(x)=2|x| | C. | f(x)=log2$\frac{1}{|x|}$ | D. | f(x)=sinx |
9.某中学安排语文、数学、英语各一名教师负责期末考试的一个考场的语文、数学、英语的监考工作,每场考试需要两名教师,则每科目的考试恰有同科目的教师监考的概率为( )
| A. | $\frac{5}{9}$ | B. | $\frac{8}{27}$ | C. | $\frac{4}{27}$ | D. | $\frac{2}{9}$ |

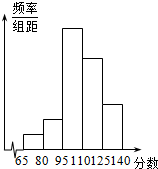 为了解某校高二学生联考数学成绩分布,从该校参加联科的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图,若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频率是6,则样本容量为40;众数为102.5.
为了解某校高二学生联考数学成绩分布,从该校参加联科的学生数学成绩中抽取一个样本,并分成5组,绘成如图所示的频率分布直方图,若第一组至第五组数据的频率之比为1:2:8:6:3,最后一组数据的频率是6,则样本容量为40;众数为102.5.