题目内容

2．Sn为等差数列{an}的前n项和，若a3+a11=12，则S13=（　　）
A．60B．78C．156D．不确定

分析 利用等差数列{an}的性质可得：a3+a11=12=a1+a13，再利用等差数列的前n项和公式即可得出．

解答 解：由等差数列{an}的性质可得：a3+a11=12=a1+a13，
则S13=$\frac{13（{a}_{1}+{a}_{13}）}{2}$=$\frac{13×12}{2}$=78．
故选：B．

点评 本题考查了等差数列的通项公式的性质及其前n项和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
12．数列{an}的前n项和为Sn，Sn+an=-$\frac{1}{2}$n2-$\frac{3}{2}$n+1（n∈N*）．
（Ⅰ）设bn=an+n，证明：数列{bn}是等比数列；
（Ⅱ）求数列{（2n-3）bn}的前n项和Tn，并证明Tn$∈[-\frac{1}{2}，1）$．
13．设A={x|x2-5x+4≤0}，B={x|x2-2ax+a+2＜0}
（1）用区间表示A；    
（2）若B⊆A，求实数a的取值范围．
10．圆（x-4）2+y2=9和圆x2+（y-3）2=4的公切线有（　　）
A．1条B．2条C．3条D．4条
17．一个几何体的三视图如图所示，则该几何体的体积是$\frac{20}{3}$．
7．已知全集U={1，2，3，4，5}，A={1，2，3}，那么∁UA的子集个数有4个．
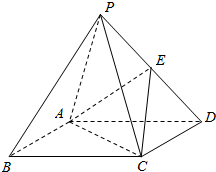14．如图，在四棱锥P-ABCD中，底面ABCD是正方形，顶点P在底顶上的射影是底面的中心，E为侧棱PD的中点．
（Ⅰ）证明：PB∥平面AEC；
（Ⅱ）设AB=2$\sqrt{2}$，二面角D-AE-C为直二面角，求三棱锥E-ACD的体积．
11．关于x的不等式ax2-（a+1）x+1＜0（a＜0）的解集为{x|x＞1或x＜$\frac{1}{a}$}．
12．在一次演唱会上共10名演员，其中8人能唱歌，5人会跳舞，现要演出一个2人唱歌2人伴舞的节目，有多少选派方法．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网