一个几何体的三视图如图所示.则该几何体的体积是$\frac{20}{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

17．一个几何体的三视图如图所示，则该几何体的体积是$\frac{20}{3}$．

分析根据几何体的三视图，得出该几何体是三棱柱与四棱锥的组合体，结合图中数据，求出它的体积．

解答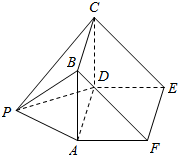解：根据几何体的三视图，得；
该几何体是三棱柱ABF-DCE与四棱锥P-ABCD的组合体，
如图所示；
则该几何体的体积为
V=$\frac{1}{3}$×2²×2+$\frac{1}{2}$×2×2×2=$\frac{20}{3}$．
故答案为：$\frac{20}{3}$．

点评本题考查了几何体三视图的应用问题，也考查了空间想象能力的应用问题，是基础题目．

练习册系列答案

8．函数的定义域是$y=（x-1）^{0}+\sqrt{lo{g}_{\frac{2}{3}}（3x-2）}$（　　）

5．下列命题是真命题的有（　　）
①“等边三角形的三个内角均为60°”的逆命题；
②“全等三角形的面积相等”的否命题．
③“若k＞0，则方程x²+2x-k=0有实根”的逆否命题．

12．下列函数中为偶函数且在（0，+∞）上是增函数的是（　　）

2．S_n为等差数列{a_n}的前n项和，若a₃+a₁₁=12，则S₁₃=（　　）

9．计算以下式子的值：
（1）$\root{3}{（-4）^{3}}-（\frac{1}{2}）^{0}+0.2{5}^{\frac{1}{2}}×（\frac{-1}{\sqrt{2}}）^{-4}$；
（2）$log{\;}_381+lg20+lg5+{4^{log{\;}_42}}+log{\;}_51$．

6．已知等差数列{a_n}的公差d不为0，且a₂，a₄，a₅成等比数列，则$\frac{{a}_{1}}{d}$=-$\frac{5}{2}$．

7．函数f（x）=ln（sin²x-cos²x）的定义域是（　　）

	A．	2kπ-$\frac{3π}{4}$＜x＜2kπ+$\frac{π}{4}$，k∈Z		B．	2kπ+$\frac{π}{4}$＜x＜2k$π+\frac{5π}{4}$，k∈Z
	C．	k$π-\frac{π}{4}$＜x＜k$π+\frac{π}{4}$，k∈Z		D．	k$π+\frac{π}{4}$＜x＜k$π+\frac{3π}{4}$，k∈Z

试题分类