题目内容
14.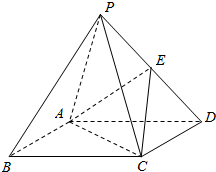 如图,在四棱锥P-ABCD中,底面ABCD是正方形,顶点P在底顶上的射影是底面的中心,E为侧棱PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,顶点P在底顶上的射影是底面的中心,E为侧棱PD的中点.(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设AB=2$\sqrt{2}$,二面角D-AE-C为直二面角,求三棱锥E-ACD的体积.
分析 (Ⅰ)连结AC、BD,交于点O,连结OE,由三角形中位线定理得OE∥PB,由此能证明PB∥平面AEC.
(Ⅱ)以O为原点,OC为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出三棱锥E-ACD的体积.
解答  (Ⅰ)证明:连结AC、BD,交于点O,连结OE,
(Ⅰ)证明:连结AC、BD,交于点O,连结OE,
∵底面ABCD是正方形,E为侧棱PD的中点,
∴OE∥PB,
∵OE?平面AEC,PB?平面AEC,
∴PB∥平面AEC.
(Ⅱ)解:∵AB=2$\sqrt{2}$,底面ABCD是正方形,E为侧棱PD的中点,
二面角D-AE-C为直二面角,顶点P在底顶上的射影是底面的中心,
∴以O为原点,OC为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,
设P(0,0,t),则A(-2,0,0),C(2,0,0),D(0,2,0),E(0,1,$\frac{t}{2}$),
$\overrightarrow{AC}$=(4,0,0),$\overrightarrow{AE}$=(2,1,$\frac{t}{2}$),$\overrightarrow{AD}$=(2,2,0),
设平面ACE的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=4x=0}\\{\overrightarrow{n}•\overrightarrow{AE}=2x+y+\frac{t}{2}z=0}\end{array}\right.$,取z=2,得$\overrightarrow{n}$=(0,-t,2),
设平面ADE的法向量$\overrightarrow{m}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AD}=2a+2b=0}\\{\overrightarrow{m}•\overrightarrow{AE}=2a+b+\frac{t}{2}c=0}\end{array}\right.$,取a=1,得$\overrightarrow{m}$=(1,-1,-$\frac{2}{t}$),
∵二面角D-AE-C为直二面角,
∴$\overrightarrow{n}•\overrightarrow{m}$=t-$\frac{4}{t}$=0,解得t=2或t=-2(舍),
∴OP=2,作EF⊥平面ACD,垂足为F,则EF=$\frac{1}{2}OP=1$,
${S}_{△ACD}=\frac{1}{2}×2\sqrt{2}×2\sqrt{2}$=4,
∴三棱锥E-ACD的体积V=$\frac{1}{3}×EF×{S}_{△ACD}$=$\frac{1}{3}×1×4$=$\frac{4}{3}$.
点评 本题考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

①“等边三角形的三个内角均为60°”的逆命题;
②“全等三角形的面积相等”的否命题.
③“若k>0,则方程x2+2x-k=0有实根”的逆否命题.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 60 | B. | 78 | C. | 156 | D. | 不确定 |
| A. | 3 | B. | 2$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |