已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$的右顶点.上顶点分别为A.B.坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$.且$a=\sqrt{2}b$．(1)求椭圆C的方程,(2)过椭圆C的左焦点F1的直线l交椭圆于M.N两点.且该椭圆上存在点P.使得四边形MONP(图形上的字母按此顺序排列)恰好为平行四边形.求直线l� 题目和参考答案——青夏教育精英家教网—

题目内容

17．

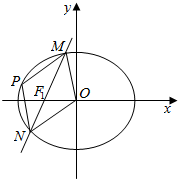已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的右顶点、上顶点分别为A、B，坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$，且$a=\sqrt{2}b$．
（1）求椭圆C的方程；
（2）过椭圆C的左焦点F₁的直线l交椭圆于M、N两点，且该椭圆上存在点P，使得四边形MONP（图形上的字母按此顺序排列）恰好为平行四边形，求直线l的方程．

分析（1）设出直线AB的方程为bx+ay-ab=0，利用坐标原点到直线AB的距离，以及$a=\sqrt{2}b$，可得椭圆的方程．
（2）求出椭圆的左焦点，设直线$l：x=my-2\sqrt{2}$，点M（x₁，y₁）、N（x₂，y₂），联立直线与椭圆方程，利用点P（x₁+x₂，y₁+y₂）在椭圆上，求出m，可得直线l的方程．

解答解：（1）设直线AB的方程为bx+ay-ab=0，坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}=\frac{ab}{{\sqrt{{a^2}+{b^2}}}}⇒\frac{{{a^2}{b^2}}}{{{a^2}+{b^2}}}=\frac{16}{3}$，又$a=\sqrt{2}b$，解得$a=4，b=2\sqrt{2}$，故椭圆的方程为$\frac{x^2}{16}+\frac{y^2}{8}=1$
（2）由（1）可求得椭圆的左焦点为${F_1}（-2\sqrt{2}，0）$，
易知直线l的斜率不为0，故可设直线$l：x=my-2\sqrt{2}$，点M（x₁，y₁）、N（x₂，y₂），
因为四边形MONP为平行四边形，所以$\overrightarrow{OP}=\overrightarrow{OM}+\overrightarrow{ON}=（{x_1}+{x_2}，{y_1}+{y_2}）⇒P（{x_1}+{x_2}，{y_1}+{y_2}）$，
联立$\left\{\begin{array}{l}x=my-2\sqrt{2}\\{x^2}+2{y^2}-16=0\end{array}\right.⇒（{m^2}+2）{y^2}-4\sqrt{2}my-8=0$⇒$\left\{\begin{array}{l}△=64（{m^2}+1）＞0\\{y_1}+{y_2}=\frac{{4\sqrt{2}m}}{{{m^2}+2}}\\{x_1}+{x_2}=m（{y_1}+{y_2}）-4\sqrt{2}\end{array}\right.⇒\left\{\begin{array}{l}{x_1}+{x_2}=\frac{{-8\sqrt{2}}}{{{m^2}+2}}\\{y_1}+{y_2}=\frac{{4\sqrt{2}m}}{{{m^2}+2}}\end{array}\right.$，
因为点P（x₁+x₂，y₁+y₂）在椭圆上，
所以${（{x_1}+{x_2}）^2}+2{（{y_1}+{y_2}）^2}=16⇒{（\frac{{-8\sqrt{2}}}{{{m^2}+2}}）^2}+2{（\frac{{4\sqrt{2}}}{{{m^2}+2}}）^2}=16⇒$$m=±\sqrt{2}$，
那么直线l的方程为$x=±\sqrt{2}y-2\sqrt{2}$．