设$\overrightarrow a.\overrightarrow b.\overrightarrow c$是单位向量.且$\overrightarrow a•\overrightarrow b=0.则({\overrightarrow a+\overrightarrow c})•({\overrightarrow b+\overrightarrow c})$的最大题目和参考答案——青夏教育精英家教网—

题目内容

20．设$\overrightarrow a，\overrightarrow b，\overrightarrow c$是单位向量，且$\overrightarrow a•\overrightarrow b=0，则（{\overrightarrow a+\overrightarrow c}）•（{\overrightarrow b+\overrightarrow c}）$的最大值为$\sqrt{2}+1$．

分析将所求展开，利用已知三个向量为单位向量，并且$\overrightarrow{a}•\overrightarrow{b}$=0，得到所求为$\overrightarrow{c}•（\overrightarrow{a}+\overrightarrow{b}）$+1，利用商量下公式求最值．

解答解：由已知得到$（\overrightarrow{a}+\overrightarrow{c}）•（\overrightarrow{b}+\overrightarrow{c}）$=$\overrightarrow{a}•\overrightarrow{b}+\overrightarrow{a}•\overrightarrow{c}+\overrightarrow{c}•\overrightarrow{b}+{\overrightarrow{c}}^{2}$=$\overrightarrow{c}•（\overrightarrow{a}+\overrightarrow{b}）$+1；
根据几何意义，|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$，设$\overrightarrow{a}+\overrightarrow{b}$与$\overrightarrow{c}$的夹角为θ，则$\overrightarrow{c}•（\overrightarrow{a}+\overrightarrow{b}）$+1=（$\sqrt{2}+1$）cosθ，所以最大值为$\sqrt{2}+1$；
故答案为：$1+\sqrt{2}$．

点评本题考查了向量的数量积公式的运用；关键是将所求变形为向量夹角的式子．

练习册系列答案

5年中考江苏13大市中考真题历年回顾精选28套卷系列答案

薪火文化假期百分百系列答案

相关题目

10．

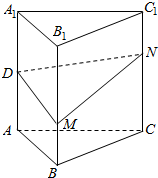如图，正三棱柱ABC-A₁B₁C₁（底面是正三角形，侧棱垂直底面）的各条棱长均相等，D为AA₁的中点．M、N分别是BB₁、CC₁上的动点（含端点），且满足BM=C₁N．当M，N运动时，下列结论中不正确的是（　　）

	A．	平面DMN⊥平面BCC₁B₁
	B．	三棱锥A₁-DMN的体积为定值
	C．	△DMN可能为直角三角形
	D．	平面DMN与平面ABC所成的锐二面角范围为（0，$\frac{π}{4}$]

11．

如图，点E，F分别在正方体ABCD-A₁B₁C₁D₁的棱DD₁、AB上，下列命题：
①A₁C⊥B₁E；
②在平面A₁B₁C₁D₁内总存在于平面B₁EF平行的直线；
③△B₁EF在侧面BCC₁B₁上的正投影是面积为定值的三角形；
④当E、F为中点时，平面B₁EF截该正方体所得的截面图形是五边形；
⑤若点P为线段EF的中点，则其轨迹为一个矩形的四周．
其中所有真命题的序号是②③④．

8．已知函数 f（x）=lnx-ax（a∈R）有两个不相等的零点 x₁，x₂（x₁＜x₂）
（I）求a的取值范围；
（Ⅱ）判断$\frac{2}{{{x_1}+{x_2}}}$与a的大小关系，并证明你的结论．

15．已知B，C两点在圆O：x²+y²=1上，A（a，0）为x轴上一点，且a＞l．给出以下命题：
①$\overrightarrow{OA}$•$\overrightarrow{OC}$的最小值为一1；
②△OBC面积的最大值为1；
③若a=$\sqrt{2}$，且直线AB，AC都与圆O相切，则△ABC为正三角形；
④若a=$\sqrt{2}$，且$\overrightarrow{AB}$=λ$\overrightarrow{BC}$（λ＞0），则当△OBC面积最大时，|AB|=$\frac{\sqrt{6}-\sqrt{2}}{2}$；
⑤若a=$\frac{\sqrt{5}}{2}$，且$\overrightarrow{AB}$=$λ\overrightarrow{BC}$，圆O上的点D满足$\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OD}$，则直线BC的斜率是$±\frac{1}{2}$．
其中正确的是⑤（写出所有正确命题的编号）．

5．设函数f（x）=|$\frac{1}{2}$x+1|+|x|（x∈R）的最小值为a．
（Ⅰ）求a；
（Ⅱ）已知两个正数m，n满足m²+n²=a，求$\frac{1}{m}$+$\frac{1}{n}$的最小值．

12．（1）证明：①C${\;}_{n}^{r}$+C${\;}_{n}^{r+1}$=C${\;}_{n+1}^{r+1}$；②C${\;}_{2n+2}^{n+1}$=2C${\;}_{2n+1}^{n}$（其中n，r∈N^*，0≤r≤n-1）；
（2）某个比赛的决赛在甲、乙两名运动员之间进行，比赛共设2n+1局，每局比赛甲获胜的概率均为p（p＞$\frac{1}{2}$），首先赢满n+1局者获胜（n∈N^*）．
①若n=2，求甲获胜的概率；
②证明：总局数越多，甲获胜的可能性越大（即甲获胜的概率越大）．

7．已知函数f（x）=$\frac{{a}^{x}-1}{{a}^{x}+1}$（a＞1）
（Ⅰ）判断函数f（x）的奇偶性
（Ⅱ）判断f（x）在（-∞，+∞）上的单调性，并用定义证明．

8．已知m∈R，n∈R，并且m+3n=1，则e^m+e³ⁿ的最小值$2\sqrt{e}$．

试题分类