题目内容
7.已知a,b,c,d均为实数,函数$f(x)=\frac{a}{3}{x^3}+\frac{b}{2}{x^2}+cx+d$(a<0)有两个极值点x1,x2(x1<x2),满足f(x2)=x1.则关于实数x的方程a[f(x)]2+bf(x)+c=0的实根个数为( )| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
分析 求导数f′(x),由题意知x1,x2是方程ax2+bx+c=0的两根,从而关于f(x)的方程a(f(x))2+bf(x)+c=0有两个根,作出草图,由图象可得答案.
解答 解:∵f′(x)=ax2+bx+c,
由题意知x1,x2是方程ax2+bx+c=0的两根,即x1,x2是函数的两个极值点,
x2>x1,从而关于f(x)的方程a[f(x)]2+b[f(x)]+c=0有两个根,
所以f(x)=x1,或f(x)=x2根据题意画图,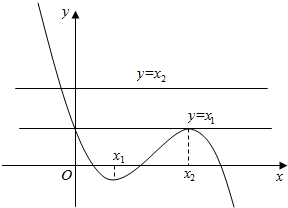
所以f(x)=x1有两个不等实根,f(x)=x2只有一个不等实根,
综上方程a[f(x)]2+bf(x)+c=0的不同实根个数为3个.
故选:C.
点评 查函数零点的概念、以及对嵌套型函数的理解,考查数形结合思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.函数f(x)对任意的a,b∈R,都有f(a+b)=f(a)+f(b)-1,并且当x>0时f(x)>1,
(1)求证:f(x)在R上是增函数;
(2)若f(2)=3,解不等式f(3m2-m-2)<3.
(1)求证:f(x)在R上是增函数;
(2)若f(2)=3,解不等式f(3m2-m-2)<3.
18.过点P(4,1)作圆C:(x-1)2+y2=1的两条切线,切点分别为A,B,则直线AB的方程为( )
| A. | 3x-y-4=0 | B. | 4x+y-4=0 | C. | 4x-y-4=0 | D. | 3x+y-4=0 |
17.曲线y=x2+3x在点A(2,10)处的切线的斜率k是( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |