题目内容

17．曲线y=x2+3x在点A（2，10）处的切线的斜率k是（　　）
A．7B．6C．5D．4

分析 根据求导公式求出y′，由导数的几何意义求出在点A（2，10）处的切线的斜率k．

解答 解：由题意知，y=x2+3x，则y′=2x+3，
∴在点A（2，10）处的切线的斜率k=4+3=7，
故选：A．

点评 本题考查求导公式和法则，以及导数的几何意义，属于基础题．

练习册系列答案
相关题目
7．已知a，b，c，d均为实数，函数$f（x）=\frac{a}{3}{x^3}+\frac{b}{2}{x^2}+cx+d$（a＜0）有两个极值点x1，x2（x1＜x2），满足f（x2）=x1．则关于实数x的方程a[f（x）]2+bf（x）+c=0的实根个数为（　　）
A．0B．2C．3D．4
8．已知角α的终边与圆x2+y2=4相交于点P（1，-$\sqrt{3}$），则sinα的值为（　　）
A．-$\frac{\sqrt{3}}{2}$B．-$\frac{1}{2}$C．$\frac{1}{2}$D．$\frac{\sqrt{3}}{2}$
5．直线x-y=0的倾斜角大小为（　　）
A．0°B．45°C．60°D．90°
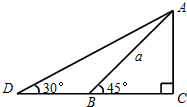12．如图，有一条长为a米的斜坡AB，它的坡角为45°，现保持坡高AC不变，将坡角改为30°，则斜坡AD的长为$\sqrt{2}$a米．
2．ξ～B（n，P），Eξ=15，Dξ=11.25，则n=（　　）
A．60B．55C．50D．45
6．若函数f（x）=（k-2013）x2+（k-2014）x+2015是偶函数，则f（x）的递增区间是[0，+∞）．
3．如图，一个几何体的三视图是三个直角三角形，则该几何体的外接球的表面积为29π．
4．证明不等式ln （x+1）≥x-$\frac{1}{2}$x2（x∈R+）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网