题目内容
15.若对任意的实数x,关于x的不等式|a-x+2|+|2a-x+1|≥|a|恒成立,则实数a的取值范围为(-∞,$\frac{1}{2}$].分析 令f(x)=|a-x+2|+|2a-x+1|,由|a-x+2|+|2a-x+1|≥|(a-x+2)-(2a-x+1)|=|a-1|,由恒成立思想可得|a|≤|a-1|,解不等式可得a的范围.
解答 解:令f(x)=|a-x+2|+|2a-x+1|,
由|a-x+2|+|2a-x+1|≥|(a-x+2)-(2a-x+1)|
=|a-1|,
当且仅当(a-x+2)(2a-x+1)≤0,取得等号,
即有f(x)的最小值为|a-1|,
由恒成立思想可得|a|≤|a-1|,
即为a2≤(a-1)2,
解得a≤$\frac{1}{2}$.
故答案为:(-∞,$\frac{1}{2}$].
点评 本题考查函数恒成立问题的解法,注意运用绝对值不等式的性质,考查运算能力,属于中档题.

练习册系列答案
相关题目
6.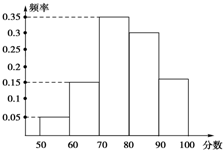 某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )
某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )
 某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )
某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )| A. | 18篇 | B. | 24篇 | C. | 25篇 | D. | 27篇 |
10.根据秦九韶算法求x=-1时f(x)=4x4+3x3-6x2+x-1的值,则v2为( )
| A. | -1 | B. | -5 | C. | 21 | D. | -22 |
5.直线x-y=0的倾斜角大小为( )
| A. | 0° | B. | 45° | C. | 60° | D. | 90° |