题目内容
2.已知函数f(x)=2x+33xf(x)=2x+33x,数列{an}满足a1=1,an+1=f(1an),(n∈N∗)an+1=f(1an),(n∈N∗),(1)求数列{an}的通项公式;
(2)设bn=1an−1an(n≥2)bn=1an−1an(n≥2),b1=3,Sn=b1+b2+…+bn,若Sn<m−20022Sn<m−20022对一切n∈N*成立,求最小正整数m的值.
分析 (1)由于an+1=f(1an)an+1=f(1an)=2×1an+33×1an2×1an+33×1an=an+2323利用等差数列的通项公式即可得出;
(2)n≥2,bn=1an−1an1an−1an=92(12n−1−12n+1)92(12n−1−12n+1),利用“裂项求和”与不等式的性质即可得出
解答 解:(1)an+1=f(1an)an+1=f(1an)=2×1an+33×1an2×1an+33×1an=an+2323,
∴an+1-an=2323,∴数列{an}是等差数列,首项为1,公差为2323.
∴an=1+23(n−1)an=1+23(n−1)=23n23n+1313.
(2)n≥2,bn=1an−1an1an−1an=9(2n−1)(2n+1)9(2n−1)(2n+1)=92(12n−1−12n+1)92(12n−1−12n+1),当n=1时也成立,
∴Sn=b1+b2+…+bn=9292[(1−13)+(13−15)[(1−13)+(13−15)+…+(12n−1−12n+1)](12n−1−12n+1)]=9292(1−12n+1)(1−12n+1),
若Sn<m−20022Sn<m−20022对一切n∈N*成立,
∴9292(1−12n+1)(1−12n+1)<m−20022m−20022对一切n∈N*成立,∴9292≤m−20022m−20022,解得m≥2011.
最小正整数m的值为2011.
点评 本题考查了等差数列的通项公式、“裂项求和”与不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
10.根据秦九韶算法求x=-1时f(x)=4x4+3x3-6x2+x-1的值,则v2为( )
| A. | -1 | B. | -5 | C. | 21 | D. | -22 |
17.M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x•x0+y•y0=a2与该圆的位置关系为( )
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相切或相离 |
14.抛掷一枚均匀硬币两次,已知有一次是正面向上,则另一次正面向上的概率为( )
| A. | 1212 | B. | 1414 | C. | 1313 | D. | 2323 |
11.定义在上(0,π4π4)的函数f(x)满足2f(x)<f′(x)tan2x,f′(x)是f(x)的导函数,则( )
| A. | √3√3f(π12π12)<f(π6π6) | B. | f(1414)>2f(π12)>2f(π12)sin1212 | C. | √3√3f(π8π8)>√2√2f(π6π6) | D. | √2√2f(π12π12)>f(π8π8) |
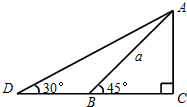 如图,有一条长为a米的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为
如图,有一条长为a米的斜坡AB,它的坡角为45°,现保持坡高AC不变,将坡角改为30°,则斜坡AD的长为