题目内容
16.已知函数f(x)=ax3,函数g(x)=x2+bx+c满足g(1)=g(3)=-6.(1)当a=-$\frac{2}{3}$时,求函数h(x)=f(x)-g(x)在[0,$\sqrt{3}$)上的最值;
(2)当x∈[-2,0]时,f(x)≥g(x)恒成立,求实数a的取值范围
附:(xa)′=axα-1,这里α∈Q.
分析 (1)由g(1)=g(3)=-6列出方程组求出b、c的值,代入h(x)化简并求出h′(x),利用导数与函数单调性的关系,求出h′(x)>0和h′(x)<0的解集,即可判断出函数h(x)的单调区间,再求出h(x)的最大值和最小值;
(2)由(1)和二次函数的单调性求出g(x)在[-2,0]上的单调性和最大值,求出f′(x)根据恒成立判断出a的符号,确定出f(x)的单调性并求出最小值,根据条件列出不等式,求出实数a的取值范围.
解答 解:(1)∵g(x)=x2+bx+c满足g(1)=g(3)=-6,
∴$\left\{\begin{array}{l}{1+b+c=-6}\\{9+3b+c=-6}\end{array}\right.$,解得b=-4,c=-3,
∴g(x)=x2-4x-3,
又a=-$\frac{2}{3}$,则h(x)=f(x)-g(x)=$-\frac{2}{3}{x}^{3}$-x2+4x+3,
∴h′(x)=-2x2-2x+4=2(-x2-x+2)=-2(x-1)(x+2),
∴当x∈[0,1)时,h′(x)>0,当x∈$(1,\sqrt{3})$时,h′(x)<0,
∴函数h(x)在[0,1)上递增,在$(1,\sqrt{3})$递减,
则当x=1时,函数h(x)取到最大值是h(1)=$\frac{16}{3}$,
又h(0)=3,h($\sqrt{3}$)=2$\sqrt{3}$>3,
∴函数h(x)在[0,$\sqrt{3}$)上的最大值是$\frac{16}{3}$,最小值是3;
(2)由(1)可得,g(x)=x2-4x-3=(x-2)2-7,
∴g(x)在[-2,0]上单调递减,最大值是g(-2)=9,
又f(x)=ax3,则f′(x)=3ax2,
∵当x∈[-2,0]时,f(x)≥g(x)恒成立,则a<0.
∴f′(x)=3ax2≥0,则f(x)在[-2,0]上单调递增,最小值是f(-2)=-8a,
∵当x∈[-2,0]时,f(x)≥g(x)恒成立,∴-8a≥9,
解得a≤$-\frac{9}{8}$,
∴实数a的取值范围是(-∞,$-\frac{9}{8}$].
点评 本题考查求导公式和法则,利用导数研究函数的单调性、最值,以及恒成立问题的转化,属于中档题.

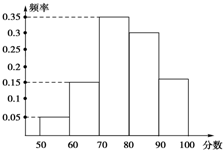 某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )
某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布直方图.已知从左往右4个小组的频率分别是0.05,0.15,0.35,0.30,那么在这次评比中被评为优秀的调查报告有(分数大于等于80分为优秀,且分数为整数)( )| A. | 18篇 | B. | 24篇 | C. | 25篇 | D. | 27篇 |
| A. | $\sqrt{3}$f($\frac{π}{12}$)<f($\frac{π}{6}$) | B. | f($\frac{1}{4}$)$>2f(\frac{π}{12})$sin$\frac{1}{2}$ | C. | $\sqrt{3}$f($\frac{π}{8}$)>$\sqrt{2}$f($\frac{π}{6}$) | D. | $\sqrt{2}$f($\frac{π}{12}$)>f($\frac{π}{8}$) |
| A. | -1或3 | B. | -3或3 | C. | 1或-1 | D. | 3或1 |
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | 0° | B. | 45° | C. | 60° | D. | 90° |
