题目内容
【题目】设命题p:函数f(x)=lg(ax2-x+16a)的定义域为R;命题q:不等式3x-9x<a对任意x∈R恒成立.
(1)如果p是真命题,求实数a的取值范围;
(2)如果命题“p或q”为真命题且“p且q”为假命题,求实数a的取值范围.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)命题p是真命题,有a>0,△<0,即求解即可.
(2)命题q是真命题,不等式3x-9x<a对一切x∈R均成立,设y=3x-9x,令t=3x>0,则y=t-t2,t>0,通过函数的最值求解a的范围,利用复合命题的真假关系求解即可.
解:(1)命题p是真命题,则ax2-x+16a>0恒成立,得到a>0,△=1-64a2<0,即a>![]() ,或a
,或a![]() (舍去),所以a的取值范围为
(舍去),所以a的取值范围为![]() .
.
(2)命题q是真命题,不等式3x-9x<a对一切x∈R均成立,
设y=3x-9x,令t=3x>0,则y=t-t2,t>0,
当![]() 时,
时,![]() ,所以
,所以![]() .
.
命题“p∨q”为真命题,“p∧q”为假命题,则p,q一真一假.
即有![]() 或
或![]() ,
,
综上,实数a的取值范围![]() .
.

 小学夺冠AB卷系列答案
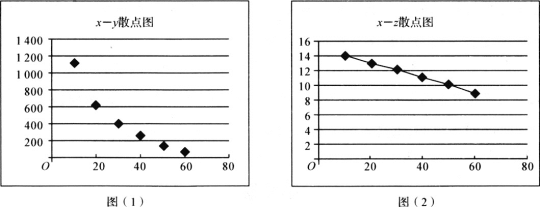
小学夺冠AB卷系列答案【题目】物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性,对某公司的该产品的销量与价格进行了统计分析,得到如下数据和散点图:
定价x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=21ny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
(参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() )
)
(Ⅰ)根据散点图判断,y与x和z与x哪一对具有的线性相关性较强(给出判断即可,不必说明理由)?
(Ⅱ)根据(Ⅰ)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为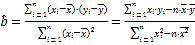 ,
,![]() .
.
【题目】近年来,随着互联网技术的快速发展,共享经济覆盖的范围迅速扩张,继共享单车、共享汽车之后,共享房屋以“民宿”、“农家乐”等形式开始在很多平台上线.某创业者计划在某景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向,此创业者对该景区附近六家“农家乐”跟踪调查了![]() 天.得到的统计数据如下表,
天.得到的统计数据如下表,![]() 为收费标准(单位:元/日),
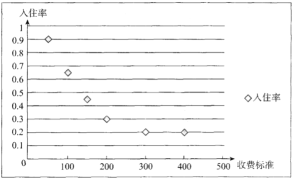
为收费标准(单位:元/日),![]() 为入住天数(单位:),以频率作为各自的“入住率”,收费标准
为入住天数(单位:),以频率作为各自的“入住率”,收费标准![]() 与“入住率”
与“入住率”![]() 的散点图如图
的散点图如图
x | 50 | 100 | 150 | 200 | 300 | 400 |
t | 90 | 65 | 45 | 30 | 20 | 20 |
(1)若从以上六家“农家乐”中随机抽取两家深入调查,记![]() 为“入住率”超过
为“入住率”超过![]() 的农家乐的个数,求
的农家乐的个数,求![]() 的概率分布列;
的概率分布列;
(2)令![]() ,由散点图判断
,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(
哪个更合适于此模型(给出判断即可,不必说明理由)?并根据你的判断结果求回归方程.(![]() 结果保留一位小数)
结果保留一位小数)
(3)若一年按![]() 天计算,试估计收费标准为多少时,年销售额
天计算,试估计收费标准为多少时,年销售额![]() 最大?(年销售额
最大?(年销售额![]() 入住率
入住率![]() 收费标准
收费标准![]() )
)
参考数据: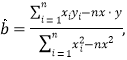
![]()
![]()
![]()