题目内容
【题目】已知△ABC中,B(-1,0),C(1,0),AB=6,点P在AB上,且∠BAC=∠PCA.
(1)求点P的轨迹E的方程;
(2)若![]() ,过点C的直线与E交于M,N两点,与直线x=9交于点K,记QM,QN,QK的斜率分别为k1,k2,k3,试探究k1,k2,k3的关系,并证明.
,过点C的直线与E交于M,N两点,与直线x=9交于点K,记QM,QN,QK的斜率分别为k1,k2,k3,试探究k1,k2,k3的关系,并证明.
【答案】(1)![]() .(2) k1+k2=2k3证明见解析;
.(2) k1+k2=2k3证明见解析;
【解析】
(1)利用已知条件判断P的轨迹为椭圆,转化求解即可.
(2)如图,设M(x1,y1),N(x2,y2),可设直线MN方程为y=k(x-1),则K(4,3k),联立直线与椭圆方程,通过韦达定理转化求解斜率关系,证明k1+k2=2k3.
解:(1)如图三角形ACP中,∠BAC=∠PCA,所以PA=PC,
所以PB+PC=PB+PA=AB=6,
所以点P的轨迹是以B,C为焦点,长轴为4的椭圆(不包含实轴的端点),
所以点P的轨迹E的方程为![]() .
.
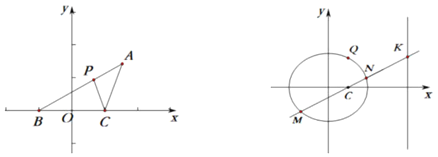
(2)k1,k2,k3的关系:k1+k2=2k3.
证明:如图,设M(x1,y1),N(x2,y2),
可设直线MN方程为y=k(x-1),则K(4,3k),
由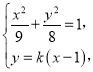 可得(9k2+8)x2-18k2x+(9k2-72)=0,
可得(9k2+8)x2-18k2x+(9k2-72)=0,
![]() ,
,![]() ,
,
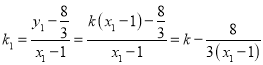 ,
,
![]() ,
,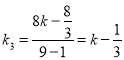 ,
,
因为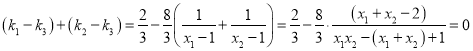 ,
,
所以:k1+k2=2k3.

【题目】为了了解![]() 地区足球特色学校的发展状况,某调查机构得到如下统计数据:
地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校 | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(Ⅰ)根据上表数据,计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并说明
,并说明![]() 与
与![]() 的线性相关性强弱(已知:
的线性相关性强弱(已知:![]() ,则认为
,则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般;
线性相关性一般;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性较弱);
线性相关性较弱);
(Ⅱ)求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 地区2019年足球特色学校的个数(精确到个)
地区2019年足球特色学校的个数(精确到个)
参考公式: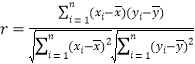 ,
,![]() ,
,![]() ,
,![]() ,
, ,
,![]() .
.
【题目】一次考试中,5名同学的数学、物理成绩如表所示:
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
![]() 请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
![]() 要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望
要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望![]() .
.
参考公式:线性回归方程![]() ;,其中
;,其中![]() ,
,![]() .
.
【题目】在![]() 中国北京世界园艺博览会期间,某工厂生产
中国北京世界园艺博览会期间,某工厂生产![]() 、
、![]() 、
、![]() 三种纪念品,每一种纪念品均有精品型和普通型两种,某一天产量如下表:(单位:个)
三种纪念品,每一种纪念品均有精品型和普通型两种,某一天产量如下表:(单位:个)
纪念品 | 纪念品 | 纪念品 | |
精品型 |
|
|
|
普通型 |
|
|
|
现采用分层抽样的方法在这一天生产的纪念品中抽取![]() 个,其中
个,其中![]() 种纪念品有
种纪念品有![]() 个.
个.
(1)求![]() 的值;
的值;
()从![]() 种精品型纪念品中抽取
种精品型纪念品中抽取![]() 个,其某种指标的数据分别如下:
个,其某种指标的数据分别如下:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,把这
,把这![]() 个数据看作一个总体,其均值为
个数据看作一个总体,其均值为![]() ,方差为
,方差为![]() ,求
,求![]() 的值;
的值;
(3)用分层抽样的方法在![]() 种纪念品中抽取一个容量为
种纪念品中抽取一个容量为![]() 的样木,从样本中任取
的样木,从样本中任取![]() 个纪念品,求至少有
个纪念品,求至少有![]() 个精品型纪念品的概率.
个精品型纪念品的概率.