Question

【题目】如图,四棱锥的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=,E为PC的中点.

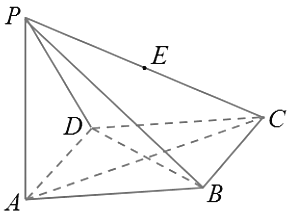
(1)求直线DE与平面PAC所成角的大小；

(2)求二面角E-AD-C平面角的正切值；

(3)在线段PC上是否存在一点M,使PC⊥平面MBD成立.如果存在,求出MC的长；如果不存在,请说明理由

Answer 1

【答案】（1）（2）2（3）

【解析】

（1）连接AC,BD交于O，连接EO，可证明DO是平面PAC的垂线，即可得到

线面角为，解三角形即可求解（2）作交AD于F, 连接EF，可证明就是二面角E-AD-C的平面角，解三角形即可求解（3）过O作于M，可证明PC⊥平面MBD成立，根据中位线确定M点位置，即可求出CM的长.

（1） 连接AC,BD,

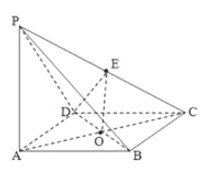
则由PA⊥底面ABCD，得平面PAC⊥底面ABCD于AC,

又由底面ABCA为菱形可得BD⊥AC于O，

平面PAC.

连接OE，则OE为DE在平面PAC上的射影，

即为DE与平面PAC所成的角.

E为PC中点可得,

由菱形性质可得，在中，

，

在中，，

.

（2）因为，PA⊥底面ABCD，

所以底面ABCD，

作交AD于F, 连接EF,

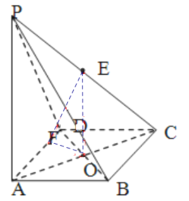
则，

所以就是二面角E-AD-C的平面角，

由ABCD是菱形，且，得，

又，

在中，.

（3）过O作于M,

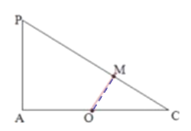
则由PA⊥底面ABCD可得平面PAC⊥底面ABCD于AC,

又底面ABCD，

平面PAC

,

而由平面PAC且，

可得平面MBD

故在线段PC上存在一点M,使PC⊥平面MBD成立，

此时，所以M是CE的中点，

故

在可解得，所以,

在中，

所以.