题目内容
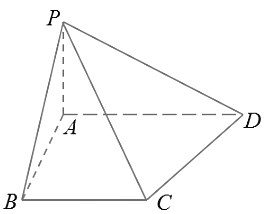
【题目】设圆![]() 的圆心在
的圆心在![]() 轴的正半轴上,与
轴的正半轴上,与![]() 轴相交于点
轴相交于点![]() ,且直线
,且直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 与圆
与圆![]() 交于
交于![]() 两点,那么以
两点,那么以![]() 为直径的圆能否经过原点,若能,请求出直线
为直径的圆能否经过原点,若能,请求出直线![]() 的方程;若不能,请说明理由.
的方程;若不能,请说明理由.
【答案】(1)![]() ;(2)能,
;(2)能,![]() 或
或![]() .
.
【解析】
(1)设圆心![]() ,
,![]() ,半径为
,半径为![]() ,由垂径定理列关于
,由垂径定理列关于![]() 与
与![]() 的方程,结合点在圆上联立求得
的方程,结合点在圆上联立求得![]() 与
与![]() 的值,则圆
的值,则圆![]() 的方程可求;
的方程可求;
(2)设![]() ,
,![]() ,
,![]() ,
,![]() 是直线
是直线![]() 与圆
与圆![]() 的交点,联立直线方程与圆的方程,化为关于
的交点,联立直线方程与圆的方程,化为关于![]() 的一元二次方程,利用根与系数的关系结合中点坐标公式可得
的一元二次方程,利用根与系数的关系结合中点坐标公式可得![]() 的中点
的中点![]() 的坐标,假如以
的坐标,假如以![]() 为直径的圆过原点,则
为直径的圆过原点,则![]() ,由此列式求解
,由此列式求解![]() 值,则直线
值,则直线![]() 的方程可求.
的方程可求.
(1)设圆心![]() ,半径为
,半径为![]() ,由垂径定理得
,由垂径定理得
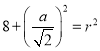 且
且![]()
解得![]() ,
,
∴圆![]() 的方程为
的方程为![]() ;
;
(2)设![]() 是直线
是直线![]() 与圆
与圆![]() 的交点,
的交点,
将![]() 代入圆
代入圆![]() 的方程得:
的方程得:![]()
![]()
∴![]() ,
,![]()
∴![]() 的中点为
的中点为![]() .
.
以![]() 为直径的圆能过原点,则
为直径的圆能过原点,则![]() ,
,
∵圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴![]() .
.
∴![]() ,解得
,解得![]() ,
,
经检验![]() 时,直线
时,直线![]() 与圆
与圆![]() 均相交,
均相交,
∴![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
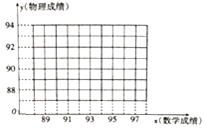
【题目】一次考试中,5名同学的数学、物理成绩如表所示:
学生 |
|
|
|
|
|
数学 | 89 | 91 | 93 | 95 | 97 |
物理 | 87 | 89 | 89 | 92 | 93 |
![]() 请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
请在图中的直角坐标系中作出这些数据的散点图,并求出这些数据的回归方程;
![]() 要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望
要从4名数学成绩在90分以上的同学中选2名参加一项活动,以X表示选中的同学的物理成绩高于90分的人数,求随机变量X的分布列及数学期望![]() .
.
参考公式:线性回归方程![]() ;,其中
;,其中![]() ,
,![]() .
.