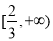题目内容
18.已知x,y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤4\\ y≥1\end{array}$,且z=$\frac{1}{2}$x+y的最大值是M,最小值是m,若 Ma+mb=3(a,b均为正实数),则$\frac{2}{a}$+$\frac{1}{b}$的最小值为( )| A. | 4 | B. | $\frac{9}{2}$ | C. | 8 | D. | 9 |
分析 利用线性规划求出M,m,得到ab的方程,然后利用基本不等式求解$\frac{2}{a}$+$\frac{1}{b}$的最小值.
解答 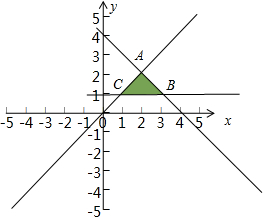 解:由题$\left\{\begin{array}{l}x-y≥0\\ x+y≤4\\ y≥1\end{array}\right.$的可行域如图:可得A(2,2),B(3,1),C(1,1);
解:由题$\left\{\begin{array}{l}x-y≥0\\ x+y≤4\\ y≥1\end{array}\right.$的可行域如图:可得A(2,2),B(3,1),C(1,1);
z=$\frac{1}{2}$x+y经过A取得最大值是M,经过C取得最小值是m,
可求得,$M=3,m=\frac{3}{2}$,
从而$a+\frac{b}{2}=1$,
$\frac{2}{a}+\frac{1}{b}=(\frac{2}{a}+\frac{1}{b})(a+\frac{b}{2})=\frac{5}{2}+\frac{b}{a}+\frac{a}{b}≥\frac{5}{2}+2=\frac{9}{2}$,
当且仅当$a=b=\frac{2}{3}$时取“=”,
故选B.
点评 本小题是线性规划的简单应用,对可行域的求取、对目标函数的理解都是考生必须掌握的基本技能,而且本题另外的一个重要考点是基本不等式的应用,此类问题也是非常典型的常规问题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
3.5名学生和2名老师排成一排照相,2名老师不在两边且不相邻的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
7.函数y=(2x-1)ex的图象是( )
| A. |  | B. |  | C. |  | D. |  |
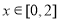 时,函数
时,函数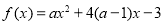 在
在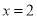 时取得最大值,则
时取得最大值,则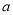 的取值范围是( )
的取值范围是( )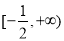 B.
B.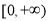
 D.
D.