题目内容
10.在平面直接坐标系中,若P(x,y)满足$\left\{\begin{array}{l}x-4y+4≤0\\ 2x+y-10≤0\\ 5x-2y+2≥0\end{array}\right.$,则当xy取得最大值时,点P的坐标是$(\frac{5}{2},5)$.分析 画出满足条件的平面区域,问题转化为z=x(10-2x)=-2x2+10x(2≤x≤4),求出函数的最值即可.
解答 解:画出满足条件的平面区域,如图示: ,
,
令z=xy,由可行域可知其在第一象限,
故z=xy可看成从点P(x,y)向x轴,y轴引垂线段,所围成矩形的面积,
故其可能取最大值的位置应在线段2x+y=10(2≤x≤4)上,
z=x(10-2x)=-2x2+10x(2≤x≤4),
当$x=\frac{5}{2},y=5$时z取最大值,此时$P(\frac{5}{2},5)$.
点评 本小题是线性规划的简单应用,对可行域的求取、对目标函数的理解都是考生必须掌握的基本技能.

练习册系列答案
相关题目
18.已知x,y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤4\\ y≥1\end{array}$,且z=$\frac{1}{2}$x+y的最大值是M,最小值是m,若 Ma+mb=3(a,b均为正实数),则$\frac{2}{a}$+$\frac{1}{b}$的最小值为( )
| A. | 4 | B. | $\frac{9}{2}$ | C. | 8 | D. | 9 |
5.函数f(x)=x•e|x|的大致图象为( )
| A. |  | B. |  | C. |  | D. |  |
15.将函数y=sin(2x-ϕ)(0<ϕ<π)的图象沿x轴向左平移$\frac{π}{6}$个单位后得到的图象关于原点对称,则ϕ的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个交点与抛物线y2=8x的焦点重合,且双曲线的离心率等于$\sqrt{2}$,则该双曲线的方程为( )
| A. | x2-y2=4 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1 | D. | x2-y2=2 |
20.已知{an}为等差数列且公差d≠0,其首项a1=20,且a3,a7,a9成等比数列,Sn为{an}的前n项和,n∈N*,则S10的值为( )
| A. | -110 | B. | -90 | C. | 90 | D. | 110 |
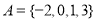 ,
,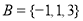 ,则
,则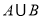 元素的个数为( )
元素的个数为( )