题目内容
9.函数f(x)是奇函数,且当x<0时,$f(x)={(\frac{1}{2})^x}$,则f(1)=-2.分析 由奇函数的性质:f(-x)=-f(x),代入解析式求出f(1)的值即可.
解答 解:因为函数f(x)是奇函数,且当x<0时,$f(x)={(\frac{1}{2})^x}$,
所以f(1)=-f(-1)=-${(\frac{1}{2})}^{-1}$=-2,
故答案为:-2.
点评 本题考查了奇函数性质的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.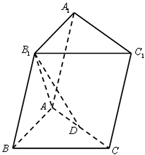 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
(Ⅰ)求证:平面ABC⊥平面ABB1A1;
(Ⅱ)求B到平面AB1D的距离.
 如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.
如图,在三棱柱ABC-A1B1C1中,B1B=B1A=BA=BC=2,∠B1BC=90°,D为AC的中点,AB⊥B1D.(Ⅰ)求证:平面ABC⊥平面ABB1A1;
(Ⅱ)求B到平面AB1D的距离.
18.已知x,y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤4\\ y≥1\end{array}$,且z=$\frac{1}{2}$x+y的最大值是M,最小值是m,若 Ma+mb=3(a,b均为正实数),则$\frac{2}{a}$+$\frac{1}{b}$的最小值为( )
| A. | 4 | B. | $\frac{9}{2}$ | C. | 8 | D. | 9 |
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个交点与抛物线y2=8x的焦点重合,且双曲线的离心率等于$\sqrt{2}$,则该双曲线的方程为( )
| A. | x2-y2=4 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{y}^{2}}{5}$-$\frac{{x}^{2}}{4}$=1 | D. | x2-y2=2 |
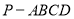 中,
中,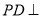 底面
底面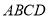 ,底面
,底面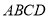 是直角梯形,
是直角梯形,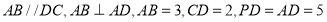 .
.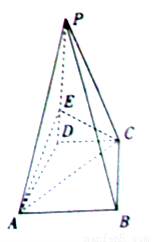
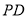 上确定一点
上确定一点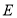 ,使得
,使得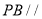 平面
平面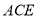 ,并求
,并求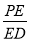 的值;
的值;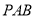 与平面
与平面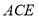 所成锐二面角的余弦值.
所成锐二面角的余弦值.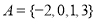 ,
,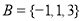 ,则
,则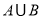 元素的个数为( )
元素的个数为( )