题目内容
13.已知x0是函数f(x)=2x+$\frac{1}{1-x}$的一个零点,若x1∈(1,x0),x2∈(x0,+∞),则$\frac{f({x}_{2})}{f({x}_{1})}$与1的大小关系为$\frac{f({x}_{2})}{f({x}_{1})}<1$.分析 先求出函数的定义域和导数,再判断出函数的单调性,由函数零点的定义即可得到结论.
解答 解:由题意得,函数f(x)的定义域是{x|x≠0},且f′(x)=2xln2+$\frac{1}{(1-x)^{2}}$>0,
∴函数f(x)在(-∞,1)、(1,+∞)上单调递增,
∵f(x0)=0,且x1∈(1,x0),x2∈(x0,+∞),
∴f(x1)<f(x0)=0<f(x2),
则$\frac{f({x}_{2})}{f({x}_{1})}<0<1$,
故答案为:$\frac{f({x}_{2})}{f({x}_{1})}<1$.
点评 本题考查了函数零点的概念,导数与函数单调性的问题,属基础题.

练习册系列答案
相关题目
18.已知x,y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤4\\ y≥1\end{array}$,且z=$\frac{1}{2}$x+y的最大值是M,最小值是m,若 Ma+mb=3(a,b均为正实数),则$\frac{2}{a}$+$\frac{1}{b}$的最小值为( )
| A. | 4 | B. | $\frac{9}{2}$ | C. | 8 | D. | 9 |
5.函数f(x)=x•e|x|的大致图象为( )
| A. |  | B. |  | C. |  | D. |  |
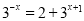 的解为_________.
的解为_________.