题目内容
自圆O外一点P引切线与圆切于点A,M为PA的中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.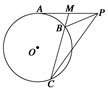

证明 ∵PA与圆相切于A,
∴MA2=MB·MC,
∵M为PA中点,∴PM=MA,
∴PM2=MB·MC,∴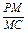 =
=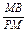 .
.
∵∠BMP=∠PMC,∴△BMP∽△PMC,
∴∠MCP=∠MPB.
∴MA2=MB·MC,
∵M为PA中点,∴PM=MA,
∴PM2=MB·MC,∴
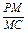 =
=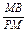 .
.∵∠BMP=∠PMC,∴△BMP∽△PMC,
∴∠MCP=∠MPB.
证明 ∵PA与圆相切于A,
∴MA2=MB·MC,
∵M为PA中点,∴PM=MA,
∴PM2=MB·MC,∴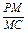 =
=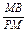 .
.
∵∠BMP=∠PMC,∴△BMP∽△PMC,
∴∠MCP=∠MPB.
∴MA2=MB·MC,
∵M为PA中点,∴PM=MA,
∴PM2=MB·MC,∴
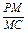 =
=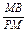 .
.∵∠BMP=∠PMC,∴△BMP∽△PMC,
∴∠MCP=∠MPB.

练习册系列答案
相关题目
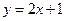 上,且到
上,且到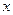 轴的距离恰等于圆的半径,在
轴的距离恰等于圆的半径,在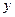 轴上截得的弦长为
轴上截得的弦长为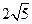 ,求此圆的方程.
,求此圆的方程.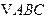 中,若两点
中,若两点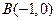 、
、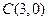 ,
,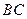 边中线
边中线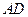 的长度为4,则点A的轨迹方程为( )
的长度为4,则点A的轨迹方程为( )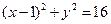
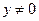 )
)
 )
)
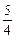 )、N(-4,
)、N(-4,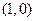 ,且总与直线
,且总与直线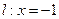 相切.
相切.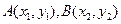 两点,当
两点,当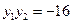 时,
时,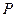 向圆
向圆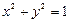 引两条切线
引两条切线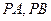 ,切点分别为
,切点分别为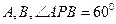 ,则
,则