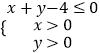题目内容
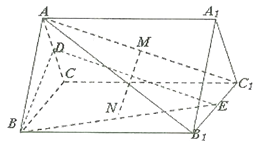
【题目】如图,四棱锥![]() 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的![]() 倍,
倍,![]() 为侧棱
为侧棱![]() 上的点.
上的点.
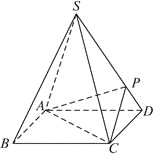
(1)求证:![]() .
.
(2)若![]() ⊥平面
⊥平面![]() ,求二面角
,求二面角![]() 的大小.
的大小.
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
【答案】(1)详见解析(2)30°(3)SE∶EC=2∶1
【解析】试题分析:(1)连BD,设AC交于BD于O,由题意知SO⊥平面ABCD.以O为坐标原点,![]() 分别为x轴、y轴、z轴正方向,建立坐标系O-xyz,设底面边长为a,求出高SO,从而得到点S与点C和D的坐标,求出向量
分别为x轴、y轴、z轴正方向,建立坐标系O-xyz,设底面边长为a,求出高SO,从而得到点S与点C和D的坐标,求出向量![]() 与
与![]() ,计算它们的数量积,从而证明出OC⊥SD,则AC⊥SD;(2)根据题意先求出平面PAC的一个法向量
,计算它们的数量积,从而证明出OC⊥SD,则AC⊥SD;(2)根据题意先求出平面PAC的一个法向量![]() 和平面DAC的一个法向量
和平面DAC的一个法向量![]() ,设所求二面角为θ,则
,设所求二面角为θ,则![]() ,从而求出二面角的大小;(3)在棱SC上存在一点E使BE∥平面PAC,根据(Ⅱ)知
,从而求出二面角的大小;(3)在棱SC上存在一点E使BE∥平面PAC,根据(Ⅱ)知![]() 是平面PAC的一个法向量,设
是平面PAC的一个法向量,设![]() ,求出
,求出![]() ,根据
,根据![]() 可求出t的值,从而即当SE:EC=2:1时,
可求出t的值,从而即当SE:EC=2:1时,![]() ,而BE不在平面PAC内,故BE∥平面PAC
,而BE不在平面PAC内,故BE∥平面PAC
试题解析:(1)证明:连BD,设AC交BD于O,由题意SO⊥AC.在正方形ABCD中,AC⊥BD,所以AC⊥平面SBD,得AC⊥SD
(2)设正方形边长a,则![]() .
.
又![]() ,所以∠SDO=60°.
,所以∠SDO=60°.
连OP,由(1)知AC⊥平面SBD,所以AC⊥OP,且AC⊥OD.所以∠POD是二面角P-AC-D的平面角.
由SD⊥平面PAC,知SD⊥OP,所以∠POD=30°,
即二面角P-AC-D的大小为30°
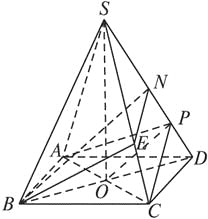
(3)在棱SC上存在一点E,使BE∥平面PAC.
由(2)可得![]() ,故可在SP上取一点N,使PN=PD.过N作PC的平行线与SC的交点即为E.连BN,在△BDN中知BN∥PO.
,故可在SP上取一点N,使PN=PD.过N作PC的平行线与SC的交点即为E.连BN,在△BDN中知BN∥PO.
又由于NE∥PC,故平面BEN∥平面PAC,得BE∥平面PAC.
由于SN∶NP=2∶1,故SE∶EC=2∶1

 一线名师权威作业本系列答案
一线名师权威作业本系列答案