题目内容
【题目】如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且 ![]() ,点C为圆O上一点,且
,点C为圆O上一点,且 ![]() .点P在圆O所在平面上的正投影为点D,PD=BD.
.点P在圆O所在平面上的正投影为点D,PD=BD. 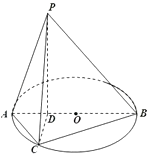
(1)求证:CD⊥平面PAB;
(2)求点D到平面PBC的距离.
【答案】
(1)解:∵AB为圆O的直径,∴AC⊥CB,
∵Rt△ABC中,由 ![]() ,∴tan∠ABC=
,∴tan∠ABC= ![]() =
= ![]() ,∠ABC=30°,
,∠ABC=30°,
∵AB=4,3AD=DB,∴DB=3, ![]() ,
,
由余弦定理,得△BCD中,CD2=DB2+BC2﹣2DBBCcos30°=3,
∴CD2+DB2=12=BC2,可得CD⊥AO.
∵点P在圆O所在平面上的正投影为点D,即PD⊥平面ABC,
又∵CD平面ABC,∴PD⊥CD,
∵PD∩AO=D得,∴CD⊥平面PAB
(2)解:由可知,PD=DB=3,且Rt△BCD中, ![]() ,
,
∴ ![]() .
.
又∵ ![]() ,
, ![]() ,
, ![]() ,
,
∴△PBC为等腰三角形,可得 ![]() .
.
设点D到平面PBC的距离为d,由VP﹣BDC=VD﹣PBC,得
![]() ,解之得
,解之得 ![]()
【解析】(1)由AB是圆的直径,得到AC⊥CB,结合BC= ![]() AC算出∠ABC=30°,进而得到
AC算出∠ABC=30°,进而得到 ![]() .△BCD中用余弦定理算出CD长,从而CD2+DB2=BC2 , 可得CD⊥AO.再根据PD⊥平面ABC,得到PD⊥CD,结合线面垂直的判定定理即可证出CD⊥平面PAB;(2)根据(1)中计算的结果,利用锥体体积公式算出
.△BCD中用余弦定理算出CD长,从而CD2+DB2=BC2 , 可得CD⊥AO.再根据PD⊥平面ABC,得到PD⊥CD,结合线面垂直的判定定理即可证出CD⊥平面PAB;(2)根据(1)中计算的结果,利用锥体体积公式算出 ![]() ,而VP﹣BDC=VD﹣PDC , 由此设点D到平面PBC的距离为d,可得
,而VP﹣BDC=VD﹣PDC , 由此设点D到平面PBC的距离为d,可得 ![]() ,结合△PBC的面积可算出点D到平面PBC的距离.
,结合△PBC的面积可算出点D到平面PBC的距离.
【考点精析】通过灵活运用直线与平面垂直的判定,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题.

【题目】汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.