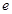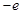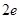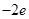题目内容
已知函数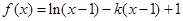
(1)求函数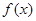 的单调区间;
的单调区间;
(2)若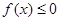 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;
(3)证明:
①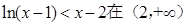 上恒成立
上恒成立
②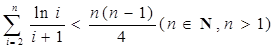
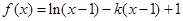
(1)求函数
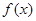 的单调区间;
的单调区间;(2)若
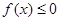 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;(3)证明:
①
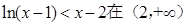 上恒成立
上恒成立②
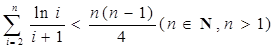
(1)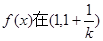 上是增函数,在
上是增函数,在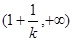 上是减函数 (2)
上是减函数 (2)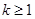 .
.
(3)见解析
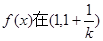 上是增函数,在
上是增函数,在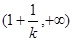 上是减函数 (2)
上是减函数 (2)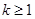 .
.(3)见解析
(1)利用导函数知识求出函数的单调区间;(2)利用分离常数法把恒成立问题转化为求函数最值问题;(3)利用放缩法求证不等式成立
(1)函数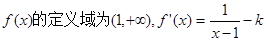 …………………1分
…………………1分
当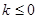 时,
时,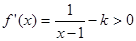 ,则
,则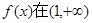 上是增函数 ………2分
上是增函数 ………2分
当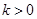 时,由
时,由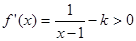 得
得
由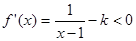 得
得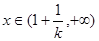 ………4分
………4分
则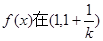 上是增函数,在
上是增函数,在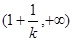 上是减函数 ……5分
上是减函数 ……5分
(采用列表的方式也要给满分)
(2)解法一:由(I)知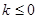 时,
时,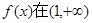 递增,而
递增,而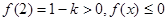 不
不
成立,故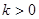 ………7分
………7分
又由(I)知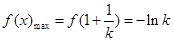 ,因为
,因为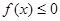 恒成立,
恒成立,
所以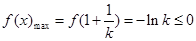 ,解得
,解得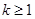 …………9分
…………9分
所以,实数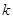 的取值范围为
的取值范围为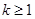 .
.
解法二(分离变量法):
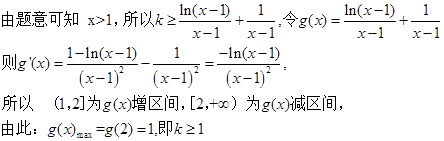 ……9分
……9分
所以,实数k的取值范围为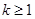 .
.
(3)①证明:由(2)知,当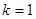 时有
时有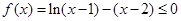 在
在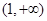 恒成立,
恒成立,
由(1)知当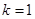 时
时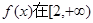 上是减函数,且
上是减函数,且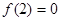 ,
,
所以,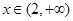 时,
时, 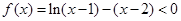 恒成立,
恒成立,
即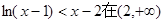 上恒成立 . ……………………11分
上恒成立 . ……………………11分
②证明:令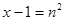 ,则
,则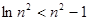 ,即
,即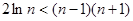 ,从而
,从而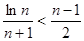 ,
,
所以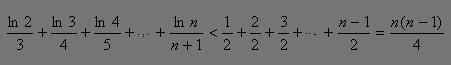
即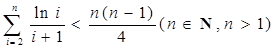
(1)函数
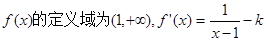 …………………1分
…………………1分当
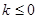 时,
时,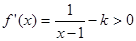 ,则
,则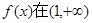 上是增函数 ………2分
上是增函数 ………2分当
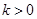 时,由
时,由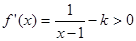 得
得
由
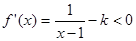 得
得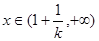 ………4分
………4分则
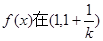 上是增函数,在
上是增函数,在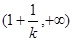 上是减函数 ……5分
上是减函数 ……5分(采用列表的方式也要给满分)
(2)解法一:由(I)知
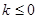 时,
时,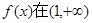 递增,而
递增,而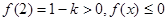 不
不 成立,故
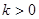 ………7分
………7分又由(I)知
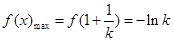 ,因为
,因为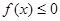 恒成立,
恒成立,所以
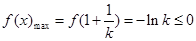 ,解得
,解得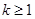 …………9分
…………9分所以,实数
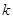 的取值范围为
的取值范围为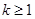 .
.解法二(分离变量法):
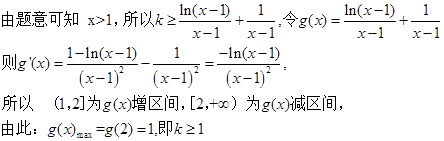 ……9分
……9分所以,实数k的取值范围为
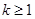 .
.(3)①证明:由(2)知,当
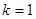 时有
时有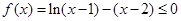 在
在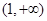 恒成立,
恒成立,由(1)知当
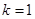 时
时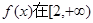 上是减函数,且
上是减函数,且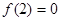 ,
,所以,
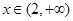 时,
时, 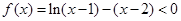 恒成立,
恒成立,即
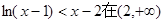 上恒成立 . ……………………11分
上恒成立 . ……………………11分②证明:令
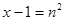 ,则
,则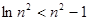 ,即
,即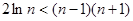 ,从而
,从而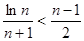 ,
,所以
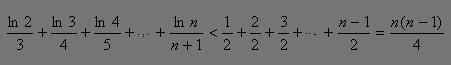
即
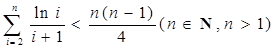

练习册系列答案
相关题目
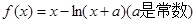 .
.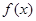 的单调区间;
的单调区间;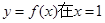 处取得极值时,若关于
处取得极值时,若关于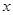 的方程
的方程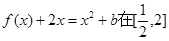 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数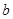 的取值范围;
的取值范围;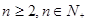 时,有
时,有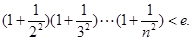
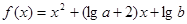 满足
满足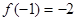 且对于任意
且对于任意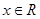 , 恒有
, 恒有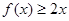 成立
成立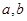 的值; (2)解不等式
的值; (2)解不等式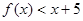
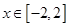 时,函数
时,函数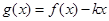 是单调函数,求实数
是单调函数,求实数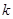 的取值范围。
的取值范围。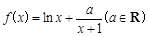 .
.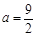 时,如果函数
时,如果函数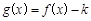 仅有一个零点,求实数
仅有一个零点,求实数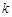 的取值范围;
的取值范围;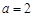 时,试比较
时,试比较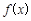 与1的大小;
与1的大小;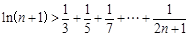
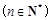 .
.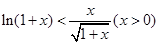
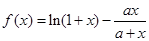 在
在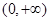 上单调递增,求实数
上单调递增,求实数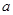 的取值范围.
的取值范围.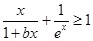 在
在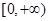 上恒成立,求实数
上恒成立,求实数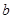 的最大值.
的最大值.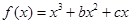 的导函数的图象关于直线x=2对称.
的导函数的图象关于直线x=2对称.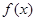 在
在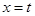 处取得极小值,记此极小值为
处取得极小值,记此极小值为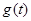 ,求
,求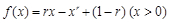 ,其中
,其中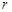 为有理数,且
为有理数,且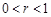 . 求
. 求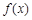 的最小值;
的最小值;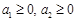 ,
,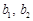 为正有理数. 若
为正有理数. 若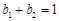 ,则
,则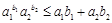 ;
;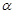 为正有理数时,有求导公式
为正有理数时,有求导公式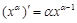 .
.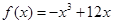 ,①求函数的单调区间;②求函数的极值,③当
,①求函数的单调区间;②求函数的极值,③当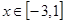 时,求函数的最大值与最小值.
时,求函数的最大值与最小值.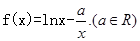
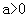 ,试判断函数
,试判断函数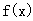 在定义域内的单调性;
在定义域内的单调性;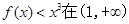 上恒成立,求实数
上恒成立,求实数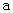 的取值范围。
的取值范围。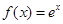 ,则
,则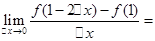 ( )
( )