题目内容
【题目】已知a∈R,函数f(x)=xln(﹣x)+(a﹣1)x.
(1)若f(x)在x=﹣e处取得极值,求函数f(x)的单调区间;
(2)求函数f(x)在区间[﹣e2 , ﹣e﹣1]上的最大值g(a).
【答案】
(1)解:f'(x)=ln(﹣x)+a,
由题意知x=﹣e时,f'(x)=0,即:f'(﹣e)=1+a=0,
∴a=﹣1
∴f(x)=xln(﹣x)﹣2x,f'(x)=ln(﹣x)﹣1
令f'(x)=ln(﹣x)﹣1=0,可得x=﹣e
令f'(x)=ln(﹣x)﹣1>0,可得x<﹣e
令f'(x)=ln(﹣x)﹣1<0,可得﹣e<x<0
∴f(x)在(﹣∞,﹣e)上是增函数,在(﹣e,0)上是减函数,
(2)解:f'(x)=ln(﹣x)+a,
∵x∈[﹣e2,﹣e﹣1],
∴﹣x∈[e﹣1,e2],
∴ln(﹣x)∈[﹣1,2],
①若a≥1,则f'(x)=ln(﹣x)+a≥0恒成立,此时f(x)在[﹣e2,﹣e﹣1]上是增函数,
fmax(x)=f(﹣e﹣1)=(2﹣a)e﹣1
②若a≤﹣2,则f'(x)=ln(﹣x)+a≤0恒成立,此时f(x)在[﹣e2,﹣e﹣1]上是减函数,
fmax(x)=f(﹣e2)=﹣(a+1)e2
③若﹣2<a<1,则令f'(x)=ln(﹣x)+a=0可得x=﹣e﹣a
∵f'(x)=ln(﹣x)+a是减函数,
∴当x<﹣e﹣a时f'(x)>0,当x>﹣e﹣a时f'(x)<0
∴f(x)在(﹣∞,﹣e)[﹣e2,﹣e﹣1]上左增右减,
∴fmax(x)=f(﹣e﹣a)=e﹣a,
综上: 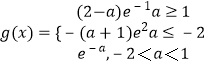
【解析】(1)先对函数y=f(x)进行求导,然后令导函数大于0(或小于0)求出x的范围,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,即可得到答案.(2)先研究f(x)在区间[﹣e2 , ﹣e﹣1]上的单调性,再利用导数求解f(x)在区间[﹣e2 , ﹣e﹣1]上的最大值问题即可,故只要先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值即得.
【考点精析】掌握利用导数研究函数的单调性和函数的极值是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;极值反映的是函数在某一点附近的大小情况.
在这个区间单调递减;极值反映的是函数在某一点附近的大小情况.