题目内容
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,BC=2 ![]() .
. 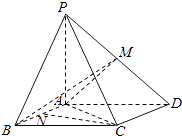
(1)求证:CD⊥平面PAC;
(2)如果如果N是棱AB上一点,且直线CN与平面MAB所成角的正弦值为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)证明:连结AC.因为在△ABC中,AB=AC=2, ![]() ,
,
所以AB2+AC2=BC2,所以AB⊥AC.
因为AB∥CD,所以AC⊥CD.
又因为PA⊥底面ABCD,所以PA⊥CD.
因为AC∩PA=A,
所以CD⊥平面PAC.
(2)解:如图,以A为原点,AB,AC,AP所在直线分别为x,y,z轴,建立空间直角坐标系.
则A(0,0,0),P(0,0,2),B(2,0,0),C(0,2,0),D(﹣2,2,0),因为M是棱PD的中点,所以M(﹣1,1,1).
所以 ![]() ,
,
设 ![]() =(x,y,z)为平面MAB的法向量,
=(x,y,z)为平面MAB的法向量,
则 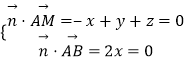 ,
,
令y=1,得平面MAB的法向量 ![]() =(0,1,﹣1),
=(0,1,﹣1),
因为N是在棱AB上一点,所以设N(x,0,0), ![]() =(﹣x,2,0).
=(﹣x,2,0).
因为直线CN与平面MAB所成角的正弦值为 ![]() ,
,
设直线CN与平面MAB所成角为α,
则sinα=|cos< ![]() >|=
>|= 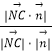 =
= ![]() =
= ![]() ,
,
解得x=1,即AN=1,NB=1,所以 ![]() =1.
=1.
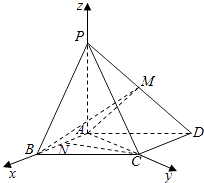
【解析】(1)连结AC,由勾股定理得AB⊥AC,从而AC⊥CD,由线面垂直得PA⊥CD,由此能证明CD⊥平面PAC.(2)以A为原点,AB,AC,AP所在直线分别为x,y,z轴,建立空间直角坐标系,由直线CN与平面MAB所成角的正弦值为 ![]() ,利用向量法能求出
,利用向量法能求出 ![]() 的值.
的值.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则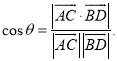 .
.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
分 组 | 频 数 | 频 率 |
[0,10) | 0.05 | |
[10,20) | 0.10 | |
[20,30) | 30 | |
[30,40) | 0.25 | |
[40,50) | 0.15 | |
[50,60] | 15 | |
合 计 | n | 1 |
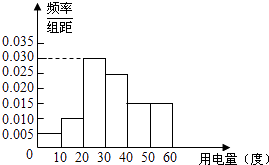
(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.
