题目内容
【题目】如图,在四边形![]() 中,
中, ![]() ,
, ![]() 平分
平分![]() ,
, ![]() ,
,
![]() ,
, ![]() 的面积为
的面积为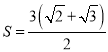 ,
, ![]() 为锐角.
为锐角.

(Ⅰ)求![]() ;
;
(Ⅱ)求![]() .
.
【答案】(I) ![]() . (II)
. (II) ![]() .
.
【解析】试题分析: (I)在![]() 中,由三角形的面积公式可求得
中,由三角形的面积公式可求得![]() ,再利用余弦定理求出
,再利用余弦定理求出![]() ;(Ⅱ)在
;(Ⅱ)在![]() 中,由正弦定理求出
中,由正弦定理求出![]() 和
和![]() ,根据题意
,根据题意![]() 平分
平分![]() ,
, ![]() ,在
,在![]() 和
和![]() 中分别写出正弦定理,得出比例关系,求出
中分别写出正弦定理,得出比例关系,求出![]() .
.
试题解析:(I)在![]() 中,
中,
 .
.
因为![]() ,所以
,所以![]() .
.
因为![]() 为锐角,所以
为锐角,所以![]() .
.
在![]() 中,由余弦定理得
中,由余弦定理得![]()
![]()
![]()
所以CD的长为![]() .
.
(II)在![]() 中,由正弦定理得
中,由正弦定理得![]()
即![]() ,解得
,解得![]()
![]() ,
, ![]() 也为锐角.
也为锐角.
![]() .
.
在![]() 中,由正弦定理得
中,由正弦定理得![]()
即 ![]() ①
①
在![]() 中,由正弦定理得
中,由正弦定理得![]()
即![]() ②
②
![]()
![]() 平分
平分![]() ,
, ![]()
![]()
由①②得![]() ,解得
,解得![]()
因为![]() 为锐角,所以
为锐角,所以![]() .
.
点睛: 解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:
第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向.
第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化.
第三步:求结果.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目