题目内容
【题目】选修4-5：不等式选讲
已知函数
（Ⅰ）求不等式
的解集；
（Ⅱ）已知函数
的最小值为
，若实数
且
，求
的
最小值．
【答案】（Ⅰ）
（Ⅱ）9.
【解析】试题分析: （Ⅰ）利用零点分段将函数
去掉绝对值化简, 进而求出不等式
的解集；（Ⅱ）根据绝对值不等式的性质求出函数的最小值,再根据基本不等式求出
的
最小值．
试题解析:（Ⅰ）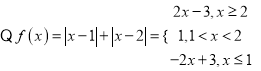
，或
，或
解得
或
不等式
的解集为
（Ⅱ）
函数
的最小值为
当且仅当
时等号成立
故
的最小值为9.
点睛: 含绝对值不等式的解法有两个基本方法，一是运用零点分区间讨论，二是利用绝对值的几何意义求解．法一是运用分类讨论思想，法二是运用数形结合思想，将绝对值不等式与函数以及不等式恒成立交汇、渗透，解题时强化函数、数形结合与转化化归思想方法的灵活应用，这是命题的新动向．
练习册系列答案
阅读快车系列答案
相关题目
