题目内容
【题目】已知曲线E上任意一点P到两个定点 
和 
的距离之和为4，
（1）求动点P的方程；
（2）设过（0，﹣2）的直线l与曲线E交于C、D两点，且 
（O为坐标原点），求直线l的方程．
【答案】
（1）解：根据椭圆的定义，可知动点M的轨迹为椭圆
其中a=2， 
，则 
，
所以动点P的轨迹方程为 
（2）解：当直线l的斜率不存在时，不满足题意，
当直线l的斜率存在时，设直线l的方程为y=kx﹣2，设C（x1，y1），D（x2，y2），
∵ 
，
∴x1x2+y1y2=0，
∵y1=kx1﹣2，y2=kx2﹣2，
∴y1y2=k2x1x2﹣2k（x1+x2）+4，
∴（1+k2）x1x2﹣2k（x1+x2）+4=0①
由方程组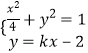 
得（1+4k2）x2﹣16kx+12=0，
则 
， 
，
代入①，得 
，
即k2=4，解得，k=2或k=﹣2，
所以，直线l的方程是y=2x﹣2或y=﹣2x﹣2
【解析】（1）根据题中条件：“距离之和为4”结合椭圆的定义，可知动点M的轨迹为椭圆，从而即可写出动点M的轨迹方程；（2）先考虑当直线l的斜率不存在时，不满足题意，再考虑当直线l的斜率存在时，设直线l的方程为y=kx﹣2，设C（x1 ， y1），D（x2 ， y2），由向量和数量积可得：x1x2+y1y2=0，由方程组 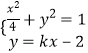，将直线的方程代入椭圆的方程，消去y得到关于x的一元二次方程，再结合根系数的关系即可求得k值，从而解决问题．
【考点精析】本题主要考查了椭圆的概念的相关知识点，需要掌握平面内与两个定点
，
的距离之和等于常数（大于
）的点的轨迹称为椭圆,这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距才能正确解答此题．
练习册系列答案
相关题目
