题目内容
设双曲线C: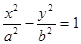 (a>0,b>0)的一个焦点坐标为(
(a>0,b>0)的一个焦点坐标为(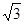 ,0),离心率
,0),离心率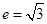 , A、B是双曲线上的两点,AB的中点M(1,2).
, A、B是双曲线上的两点,AB的中点M(1,2).
(1)求双曲线C的方程;
(2)求直线AB方程;
(3)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
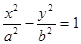 (a>0,b>0)的一个焦点坐标为(
(a>0,b>0)的一个焦点坐标为(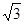 ,0),离心率
,0),离心率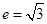 , A、B是双曲线上的两点,AB的中点M(1,2).
, A、B是双曲线上的两点,AB的中点M(1,2).(1)求双曲线C的方程;
(2)求直线AB方程;
(3)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D四点是否共圆?为什么?
(1)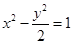 (2)
(2)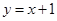 (3)是,理由见解析
(3)是,理由见解析
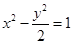 (2)
(2)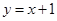 (3)是,理由见解析
(3)是,理由见解析试题分析:
(1)根据题意已知
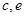 ,则利用双曲线a,b,c之间的关系与离心率的定义
,则利用双曲线a,b,c之间的关系与离心率的定义 即可求出
即可求出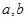 的值,进而得到双曲线的标准方程.
的值,进而得到双曲线的标准方程.(2)根据题意可得AB为双曲线的一条弦,要求弦所在直线,还需要斜率,可以采用点差法利用弦的中来求解弦的斜率,已知了弦所在直线的斜率与弦上的中点坐标,再利用直线的点斜式即可求出弦所在直线的方程.
(3)由(2)可得AB直线的方程,联立直线AB与双曲线的方程消元解二次方程即可得到A,B两点的坐标,已知AB线段的斜率与中点即可求的AB垂直平分线的直线方程,联立垂直平分线与双曲线的方程消元解二次方程即可求的CD两点的坐标.
试题解析:
(1)依题意得
 ,解得a=1. (1分)
,解得a=1. (1分)所以
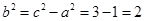 , (2分)
, (2分)故双曲线C的方程为
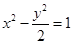 . (3分)
. (3分)(2)设
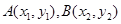 ,则有
,则有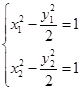 .
.两式相减得:
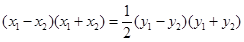 , (4分)
, (4分)由题意得
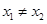 ,
,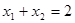 ,
,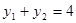 , (5分)
, (5分)所以
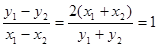 ,即
,即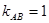 . (6分)
. (6分)故直线AB的方程为
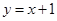 . (7分)
. (7分)(3)假设A、B、C、D四点共圆,且圆心为P. 因为AB为圆P的弦,所以圆心P在AB垂直平分线CD上;又CD为圆P的弦且垂直平分AB,故圆心P为CD中点M. (8分)
下面只需证CD的中点M满足|MA|=|MB|=|MC|=|MD|即可.
由
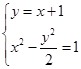 得:A(-1,0),B(3,4). (9分)
得:A(-1,0),B(3,4). (9分)由(1)得直线CD方程:
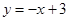 , (10分)
, (10分)由
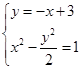 得:C(-3+
得:C(-3+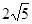 ,6-
,6-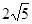 ),D(-3-
),D(-3-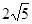 ,6+
,6+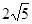 ), (11分)
), (11分)所以CD的中点M(-3,6). (12分)
因为
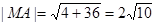 ,
,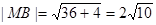 ,
,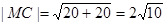 ,
,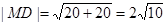 , (13分)
, (13分)所以
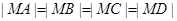 ,
,即 A、B、C、D四点在以点M(-3,6)为圆心,
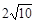 为半径的圆上. (14分)
为半径的圆上. (14分)
练习册系列答案
相关题目
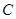 :
: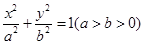 的右焦点为
的右焦点为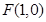 ,短轴的一个端点
,短轴的一个端点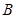 到
到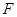 的距离等于焦距.
的距离等于焦距.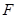 的直线
的直线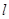 与椭圆
与椭圆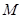 ,
,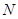 ,是否存在直线
,是否存在直线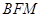 与△
与△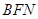 的面积比值为
的面积比值为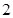 ?若存在,求出直线
?若存在,求出直线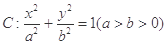 的离心率为
的离心率为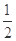 ,以原点
,以原点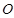 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线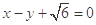 相切。
相切。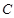 的标准方程;
的标准方程;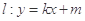 与椭圆
与椭圆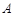 、
、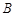 两点,且
两点,且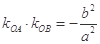 ,试判断
,试判断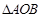 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由. 和
和 ,且|
,且| )在该椭圆上.
)在该椭圆上. 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 A
A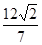 ,求以
,求以 的离心率是
的离心率是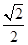 ,
, 分别是椭圆
分别是椭圆 的左、右两个顶点,点
的左、右两个顶点,点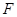 是椭圆
是椭圆 是
是 轴上位于
轴上位于 右侧的一点,且满足
右侧的一点,且满足 .
.
 ,再作直线
,再作直线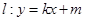 与椭圆
与椭圆 ,直线
,直线 交直线
交直线 .求证:以线段
.求证:以线段 为直径的圆恒过定点,并求出定点的坐标.
为直径的圆恒过定点,并求出定点的坐标.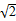 的圆C与直线y=x相切于坐标原点O,椭圆
的圆C与直线y=x相切于坐标原点O,椭圆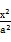 +
+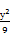 =1与圆C的一个交点到椭圆两焦点的距离之和为10.
=1与圆C的一个交点到椭圆两焦点的距离之和为10.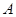 、
、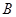 为两个定点,
为两个定点,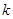 为非零常数,
为非零常数,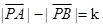 ,则动点
,则动点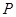 的轨迹为双曲线;
的轨迹为双曲线;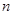 项和
项和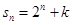 ,则必有
,则必有 ;
;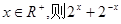 的最小值为2;
的最小值为2; 有相同的焦点;
有相同的焦点;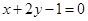 的距离的点的轨迹是抛物线.
的距离的点的轨迹是抛物线. (a为长半轴,c为半焦距)上.
(a为长半轴,c为半焦距)上.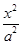 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,过F1作垂直于椭圆长轴的弦PQ,|PQ|为3.