题目内容
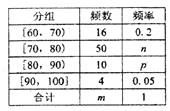
【题目】从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组,第一组![]() ;第二组
;第二组![]() ;…;第六组
;…;第六组![]() ,并据此绘制了如图所示的频率分布直方图.
,并据此绘制了如图所示的频率分布直方图.
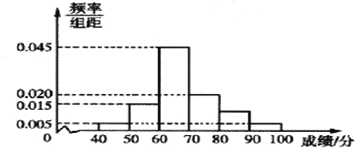
(1)求成绩在区间![]() 内的学生人数;
内的学生人数;
(2)从成绩大于等于80分的学生中随机选取2名,求至少有1名学生的成绩在区间![]() 内的概率.
内的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)由各组的频率和等于1直接列式计算成绩在![]() 的学生频率,用40乘以频率可得成绩在
的学生频率,用40乘以频率可得成绩在![]() 的学生人数;
的学生人数;
(Ⅱ)用列举法求出从成绩大于等于80分的学生中随机选2名学生的事件个数,查出至少有1名学生成绩在![]() 的事件个数,然后直接利用古典概型概率计算公式求解.
的事件个数,然后直接利用古典概型概率计算公式求解.
试题解析:(1)因为各组的频率之和为1,
所以成绩在区间![]() 内的频率为
内的频率为![]() ,
,
所以选取的40名学生中成绩在区间![]() 内的学生人数为
内的学生人数为![]() .
.
(2)设![]() 表示事件“在成绩大于等于80分的学生中随机选取2名,至少有1名学生的成绩在区间
表示事件“在成绩大于等于80分的学生中随机选取2名,至少有1名学生的成绩在区间![]() 内”,由(1)可知成绩在区间
内”,由(1)可知成绩在区间![]() 内的学生有4人,记这4名学生分别为
内的学生有4人,记这4名学生分别为![]() ,
,
成绩在区间![]() 内的学生有
内的学生有![]() (人),记这2名学生分别为
(人),记这2名学生分别为![]() ,
,
则选取2名学生的所有可能结果为![]() ,
,![]() ,
,
![]() 共15种,
共15种,
事件“至少有1名学生的成绩在区间![]() 内”的可能结果为
内”的可能结果为![]() ,
,
![]() ,共9种,
,共9种,
所以![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目