题目内容
【题目】有 ![]() 名男生,
名男生, ![]() 名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数
名女生,在下列不同条件下,求不同的排列方法种数.(最后结果化成数
字)
(1)排成前后两排,前排 ![]() 人,后排
人,后排 ![]() 人;
人;
(2)全体排成一排,甲不站在排头也不站在排尾;
(3)全体排成一排,女生必须站在一起;
(4)全体排成一排,男生不能相邻.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【解析】试题分析:(1)根据题意,将5人全排列即可,由排列数公式计算可得答案;
(2)根据题意,分2步进行分析:先分析甲,再将其余4人全排列,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(3)根据题意,用插空法分2步进行分析:先将女生看成一个整体,考虑女生之间的顺序,再将女生的整体与2名男生在一起进行全排列,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(4)根据题意,用插空法分析:先将3名女生全排列,再在女生之间及首尾空出的4个空位中任选2个空位排男生,分别求出每一步的情况数目,由分步计数原理计算可得答案.
试题解析:
(1) 分两步,第一步先从 ![]() 人中任意选出
人中任意选出 ![]() 人,第二步将这
人,第二步将这 ![]() 人排成一排.利用乘法计数原理,得到排法种数为
人排成一排.利用乘法计数原理,得到排法种数为 ![]() .
.
(2) 分两步,先从 ![]() 人中任意选出
人中任意选出 ![]() 人,再排成一排,有
人,再排成一排,有 ![]() 种方法.第二步给其余
种方法.第二步给其余 ![]() 人在后排(确定)排成一排,有
人在后排(确定)排成一排,有 ![]() 种排法.利用乘法计数原理,共有
种排法.利用乘法计数原理,共有 ![]() 种排法.
种排法.
(3) 分两步,首先从甲以外的 ![]() 人中选
人中选 ![]() 人站在排头与排尾,有
人站在排头与排尾,有 ![]() 种方法,其次连同甲的
种方法,其次连同甲的 ![]() 人在中间排成一排,有
人在中间排成一排,有 ![]() 种方法.利用乘法计数原理,有
种方法.利用乘法计数原理,有 ![]() 种排法.或先将甲放在中间
种排法.或先将甲放在中间 ![]() 个位置,有
个位置,有 ![]() 种方法,其次将连同甲的
种方法,其次将连同甲的 ![]() 人排成一排,共
人排成一排,共 ![]() 种方法,利用乘法计数原理,则共有
种方法,利用乘法计数原理,则共有 ![]() 种方法.
种方法.
(4) 分两步,首先将女生排在一起当成一个元素(捆绑法)并与其他 ![]() 个男生共
个男生共 ![]() 个元素排成
个元素排成
排,有 ![]() 种方法,再将
种方法,再将 ![]() 名女生排成一排,共
名女生排成一排,共 ![]() 种方法,利用乘法计数原理,共有
种方法,利用乘法计数原理,共有 ![]() 种方法.
种方法.

【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
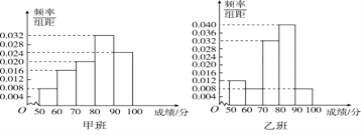
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附:.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |