题目内容
5．某班有学生50人，解甲、乙两道数学题．已知解对甲题者有34人，解对乙题者有28人，两题均对者有20人，则至少解对一题者的人数是（ ）| A． | 8 | B． | 42 | C． | 30 | D． | 22 |
分析 画出满足条件的韦恩图，分析满足条件人各个区域的人数，相加可得答案．
解答 解：如下图所示：
至少解对一题的人数为：34-20+20+28-20=42人，
故选：B．
点评 本题考查的知识点是Venn图表达集合的关系及运算，难度不大，属于基础题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
16．若函数f（x）=xsinx+cosx，则f（1），f（-$\frac{3}{2}$），f（$\frac{π}{2}$）的大小关系为（ ）
| A． | f（$\frac{π}{2}$）＞f（1）$＞f（-\frac{3}{2}）$ | B． | f（$\frac{π}{2}$）＞f（-$\frac{3}{2}$）＞f（1） | C． | f（-$\frac{3}{2}$）＞f（1）＞f（$\frac{π}{2}$） | D． | f（1）＞f（-$\frac{3}{2}$）＞f（$\frac{π}{2}$） |
13．函数y=-x2、y=$\frac{1}{x}$、y=2x+1、y=$\sqrt{x}$在x=1附近（△x很小时），平均变化率最大的一个是（ ）
| A． | y=-x2 | B． | y=$\frac{1}{x}$ | C． | y=2x+1 | D． | y=$\sqrt{x}$ |
17．函数y=$\sqrt{\frac{1}{4}-si{n}^{2}x}$+|sinx|的值域是（ ）
| A． | [-$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{2}}{2}$] | B． | [0，$\frac{\sqrt{2}}{2}$] | C． | [0，$\frac{\sqrt{3}}{2}$] | D． | [$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$] |
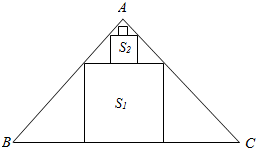在等腰直角△ABC中，∠A=90°，BC=6，△ABC中排列着内接正方形，如图所示，若正方形的面积依次为S1，S2，…，Sn，…（从大到小），其中n∈N+，则$\underset{lim}{n→∞}$（S1+S2+…+Sn）=$\frac{9}{2}$．