题目内容
16.若函数f(x)=xsinx+cosx,则f(1),f(-$\frac{3}{2}$),f($\frac{π}{2}$)的大小关系为( )| A. | f($\frac{π}{2}$)>f(1)$>f(-\frac{3}{2})$ | B. | f($\frac{π}{2}$)>f(-$\frac{3}{2}$)>f(1) | C. | f(-$\frac{3}{2}$)>f(1)>f($\frac{π}{2}$) | D. | f(1)>f(-$\frac{3}{2}$)>f($\frac{π}{2}$) |
分析 可判断函数f(x)=xsinx+cosx在其定义域上是偶函数,由导数可判断f(x)在(0,$\frac{π}{2}$]上是增函数;从而比较大小.
解答 解:∵f(x)=xsinx+cosx,
∴f(-x)=(-x)sin(-x)+cos(-x)
=xsinx+cosx=f(x),
∴函数f(x)=xsinx+cosx在其定义域上是偶函数,
f′(x)=sinx+xcosx-sinx=xcosx,
∴f(x)在(0,$\frac{π}{2}$]上是增函数;
∴f($\frac{π}{2}$)>f($\frac{3}{2}$)>f(1),
即f($\frac{π}{2}$)>f(-$\frac{3}{2}$)>f(1);
故选:B.
点评 本题考查了导数的综合应用及函数的性质的判断与应用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
1.棱长为1的正四面体的三视图中,俯视图为边长为1的正三角形,则正视图的面积的取值范围是( )
| A. | [$\frac{1}{4}$,$\frac{\sqrt{3}}{4}$] | B. | [$\frac{\sqrt{3}}{4}$,$\frac{1}{2}$] | C. | [$\frac{\sqrt{2}}{4}$,$\frac{\sqrt{6}}{6}$] | D. | [$\frac{3}{8}$,$\frac{\sqrt{3}}{4}$] |
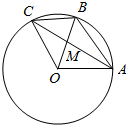 如图,A,B是单位圆上的相异两定点(O为圆心),且∠AOB=θ(θ为锐角).点C为单位圆上的动点,线段AC交线段OB于点M.
如图,A,B是单位圆上的相异两定点(O为圆心),且∠AOB=θ(θ为锐角).点C为单位圆上的动点,线段AC交线段OB于点M.