题目内容
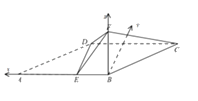
【题目】如图,四边形ABCD为平行四边形,点E在AB上,AE=2EB=2,且DE⊥AB.以DE为折痕把△ADE折起,使点A到达点F的位置,且∠FEB=60°.
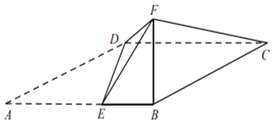
(1)求证:平面BFC⊥平面BCDE;
(2)若直线DF与平面BCDE所成角的正切值为![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)首先通过证明![]() 平面
平面![]() 证得
证得![]() .结合余弦定理和勾股定理证得
.结合余弦定理和勾股定理证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,进而证得平面
,进而证得平面![]() 平面
平面![]() .
.
(2)建立空间直角坐标系,由直线![]() 与平面
与平面![]() 所成角的正切值求得正弦值,结合直线
所成角的正切值求得正弦值,结合直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量列方程,解方程求得
的法向量列方程,解方程求得![]() 的长.由此通过平面
的长.由此通过平面![]() 和平面
和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值,进而求得其正弦值.
的余弦值,进而求得其正弦值.
(1)证明:∵DE⊥AB,∴DE⊥EB,DE⊥EF,
∴DE⊥平面BEF,∴DE⊥BF,
∵AE=2EB=2,∴EF=2,EB=1,
∵∠FEB=60°,∴由余弦定理得BF![]() ,
,
∴EF2=EB2+BF2,∴FB⊥EB,
由①②得BF⊥平面BCDE,
∴平面BFC⊥平面BCDE.
(2)解:以B为原点,BA为x轴,在平面ABCD中过点B作AB的垂线为y轴,BF为z轴,建立空间直角坐标系,
设DE=a,则D(1,a,0),F(0,0,![]() ),
),![]() (﹣1,﹣a,
(﹣1,﹣a,![]() ),
),
∵直线DF与平面BCDE所成角的正切值为![]() ,
,
∴直线DF与平面BCDE所成角的正弦值为![]() ,
,
平面BCDE的法向量![]() (0,0,1),
(0,0,1),
∴|cos![]() |
|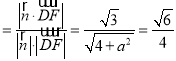 ,解得a=2,
,解得a=2,
∴D(1,2,0),C(﹣2,2,0),∴![]() (0,2,0),
(0,2,0),![]() (﹣1,﹣2,
(﹣1,﹣2,![]() ),
),
设平面EDF的法向量![]() (x,y,z),
(x,y,z),
则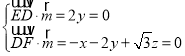 ,取z=1,得
,取z=1,得![]() (
(![]() ),
),
同理得平面DFC的一个法向量![]() (0,
(0,![]() ,2),
,2),
∴cos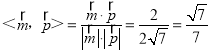 ,
,
∴二面角E﹣DF﹣C的正弦值为sin![]() .
.

【题目】学生考试中答对但得不了满分的原因多为答题不规范,具体表现为:解题结果正确,无明显推理错误,但语言不规范、缺少必要文字说明、卷面字迹不清、得分要点缺失等,记此类解答为“![]() 类解答”.为评估此类解答导致的失分情况,某市教研室做了一项试验:从某次考试的数学试卷中随机抽取若干属于“
类解答”.为评估此类解答导致的失分情况,某市教研室做了一项试验:从某次考试的数学试卷中随机抽取若干属于“![]() 类解答”的题目,扫描后由近百名数学老师集体评阅,统计发现,满分12分的题,阅卷老师所评分数及各分数所占比例大约如下表:
类解答”的题目,扫描后由近百名数学老师集体评阅,统计发现,满分12分的题,阅卷老师所评分数及各分数所占比例大约如下表:
教师评分(满分12分) | 11 | 10 | 9 |
各分数所占比例 |
|
|
|
某次数学考试试卷评阅采用“双评+仲裁”的方式,规则如下:两名老师独立评分,称为一评和二评,当两者所评分数之差的绝对值小于等于1分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于1分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分;当一、二评分数和仲裁分数差值的绝对值相同时,取仲裁分数和前两评中较高的分数的平均分为该题得分.(假设本次考试阅卷老师对满分为12分的题目中的“![]() 类解答”所评分数及比例均如上表所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
类解答”所评分数及比例均如上表所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
(1)本次数学考试中甲同学某题(满分12分)的解答属于“![]() 类解答”,求甲同学此题得分
类解答”,求甲同学此题得分![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(2)本次数学考试有6个解答题,每题满分均为12分,同学乙6个题的解答均为“![]() 类解答”,记该同学6个题中得分为
类解答”,记该同学6个题中得分为![]() 的题目个数为
的题目个数为![]() ,
,![]() ,
,![]() ,计算事件“
,计算事件“![]() ”的概率.
”的概率.
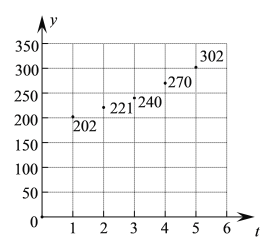
【题目】随着经济的发展和人民生活水平的提高,以及城市垃圾分类收集的实施和推广,我国居民生活垃圾的平均热值逐年.上升,垃圾焚烧发电的吨上网电量(单位:千瓦时/吨)显著增加.下表为某垃圾焚烧发电厂最近五个月的生产数据.
月份代码 |
|
|
|
|
|
吨上网电量 |
|
|
|
|
|
|
|
|
|
|
|
![]() 若从该发电厂这五个月的生产数据(吨上网电量)中任选两个,求其中至少有一个生产数据超过
若从该发电厂这五个月的生产数据(吨上网电量)中任选两个,求其中至少有一个生产数据超过![]() 的概率;
的概率;
![]() 通过散点图(如图)可以发现,变量
通过散点图(如图)可以发现,变量![]() 与
与![]() 之间的关系可以用函数
之间的关系可以用函数![]() (其中
(其中![]() 为自然对数的底数)来拟合,求常数
为自然对数的底数)来拟合,求常数![]() ,
,![]() 的值.
的值.
参考公式:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为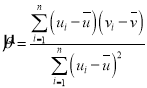 ,
,![]() .
.