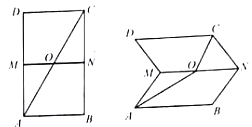
题目内容
【题目】以坐标原点为极点,以x轴的非负半轴为极轴建立极坐标系,已知曲线C的参数方程为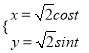 (t为参数)
(t为参数) 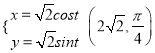 .
.
(1)若曲线C在点(1,1)处的切线为l,求l的极坐标方程;
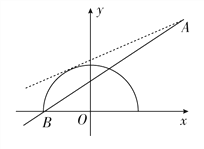
(2)若点A的极坐标为![]() ,且当参数t∈[0,π]时,过点A的直线m与曲线C有两个不同的交点,试求直线m的斜率的取值范围.
,且当参数t∈[0,π]时,过点A的直线m与曲线C有两个不同的交点,试求直线m的斜率的取值范围.
【答案】(1) ![]() ; (2)
; (2) ![]() .
.
【解析】试题分析:(1)根据极坐标与普通方程直角坐标的转化公式 即可求出切线的极坐标方程;(2)画出图象,根据数形结合,可以看出切线与割线斜率分别是最小和最大值,利用斜率坐标公式即可求出.
试题解析: (1)∵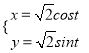 ,∴
,∴![]() ,点
,点![]() 在圆上,故切线方程为
在圆上,故切线方程为![]() ,
,
∴![]() ,l的极坐标方程为
,l的极坐标方程为![]() ;
;
(2)点A的直角坐标为![]() ,设m:
,设m: ![]() ,
,
m与半圆![]() (
(![]() )相切时,
)相切时, ![]() ,
,
∴![]() ,∴
,∴![]() 或
或![]() (舍去).
(舍去).
设点B![]() ,则
,则![]() ,故直线m的斜率的取值范围为
,故直线m的斜率的取值范围为![]() .
.

【题目】为了参加第二届全国数学建模竞赛,长郡中学在高二年级举办了一次选拔赛,共有60名高二学生报名参加,按照不同班级统计参赛人数,如表所示:
班级 | 宏志班 | 珍珠班 | 英才班 | 精英班 |
参赛人数 | 20 | 15 | 15 | 10 |
(Ⅰ)从这60名高二学生中随机选出2人,求这2人在同一班级的概率;
(Ⅱ)现从这60名高二学生中随机选出2人作为代表,进行大赛前的发言,设选出的2人中宏志班的学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】现在很多人喜欢自助游,2017年孝感杨店桃花节,美丽的桃花风景和人文景观迎来众多宾客.某调查机构为了了解“自助游”是否与性别有关,在孝感桃花节期间,随机抽取了![]() 人,得如下所示的列联表:
人,得如下所示的列联表:
赞成“自助游” | 不赞成“自助游” | 合计 | |
男性 |
| ||
女性 |
| ||
合计 |
|
(1)若在![]() 这人中,按性别分层抽取一个容量为
这人中,按性别分层抽取一个容量为![]() 的样本,女性应抽
的样本,女性应抽![]() 人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过
人,请将上面的列联表补充完整,并据此资料能否在犯错误的概率不超过![]() 前提下,认为赞成“自助游”是与性别有关系?
前提下,认为赞成“自助游”是与性别有关系?
(2)若以抽取样本的频率为概率,从旅游节大量游客中随机抽取![]() 人赠送精美纪念品,记这
人赠送精美纪念品,记这![]() 人中赞成“自助游”人数为
人中赞成“自助游”人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附: 
|
|
|
|
|
|
|
|
|
|