题目内容
在等差数列{an}中,a1>0,a2012+a2013>0,a2012•a2013<0,则使Sn>0成立的最大自然数n是( )
| A.4025 | B.4024 | C.4023 | D.4022 |
∵等差数列{an},首项a1>0,a2012+a2013>0,a2012•a2013<0,
∴a2012>0,a2013<0.
假设a2012<0<a2013,则d>0,而a1>0,可得a2012=a1+2011d>0,矛盾,故不可能.
再根据S4024=
=2012(a2012+a2013 )>0,
而S4025=4025a2013<0,
因此使前n项和Sn>0成立的最大自然数n为4024.
故选:B.
∴a2012>0,a2013<0.
假设a2012<0<a2013,则d>0,而a1>0,可得a2012=a1+2011d>0,矛盾,故不可能.
再根据S4024=
| 4024(a1+a4024) |
| 2 |
而S4025=4025a2013<0,
因此使前n项和Sn>0成立的最大自然数n为4024.
故选:B.

练习册系列答案
相关题目
 满足
满足 ,
, ,
,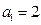 时,求
时,求 ,并由此猜想出
,并由此猜想出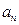 的一个通项公式;
的一个通项公式; 时,证明对所有的
时,证明对所有的 ,有
,有 ; ②
; ② .
.