题目内容
设数列 满足
满足 ,
, ,
,
(1)当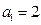 时,求
时,求 ,并由此猜想出
,并由此猜想出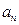 的一个通项公式;
的一个通项公式;
(2)当 时,证明对所有的
时,证明对所有的 ,有
,有
① ; ②
; ② .
.
 满足
满足 ,
, ,
,(1)当
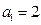 时,求
时,求 ,并由此猜想出
,并由此猜想出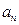 的一个通项公式;
的一个通项公式;(2)当
 时,证明对所有的
时,证明对所有的 ,有
,有①
 ; ②
; ② .
.(1)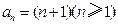 ;(2)证明见答案
;(2)证明见答案
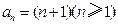 ;(2)证明见答案
;(2)证明见答案 (1)由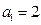 ,得
,得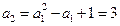 .
.
由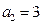 ,得
,得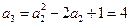 .
.
由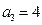 ,得
,得 .
.
由此猜想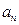 的一个通项公式:
的一个通项公式: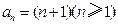 .
.
(2)证明:①用数学归纳法证明:
a.当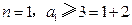 ,不等式成立.
,不等式成立.
b.假设当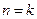 时不等式成立,即
时不等式成立,即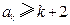 ,
,
那么,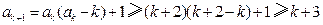 ,
,
也就是说,当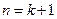 时
时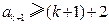 .
.
根据a和b,对于所有 ,有
,有 .
.
②由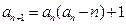 及(1),对
及(1),对 ,有
,有
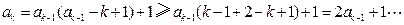
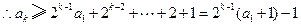 .
.
于是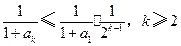 .
.
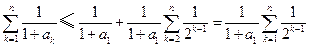
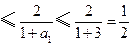 .
.
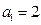 ,得
,得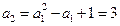 .
.由
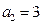 ,得
,得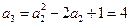 .
.由
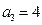 ,得
,得 .
.由此猜想
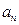 的一个通项公式:
的一个通项公式: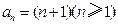 .
.(2)证明:①用数学归纳法证明:
a.当
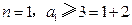 ,不等式成立.
,不等式成立.b.假设当
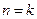 时不等式成立,即
时不等式成立,即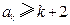 ,
,那么,
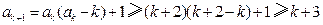 ,
,也就是说,当
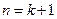 时
时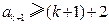 .
.根据a和b,对于所有
 ,有
,有 .
.②由
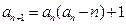 及(1),对
及(1),对 ,有
,有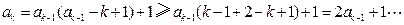
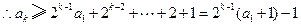 .
.于是
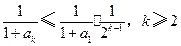 .
.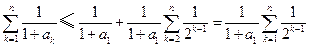
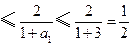 .
.
练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 ,数列{
,数列{ }是公差为d的等差数列,数列{
}是公差为d的等差数列,数列{ }是公比为q的等比数列(q≠1,
}是公比为q的等比数列(q≠1, ),若
),若 ,
,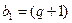 ,
, .
. }的前n项和为
}的前n项和为 ,对
,对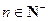 都有
都有 …
… 求
求 .
.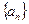 的通项公式是
的通项公式是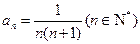 ,则
,则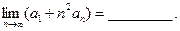
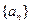 中,
中, ,
, ,
,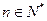 ,其中
,其中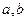 为常数,则
为常数,则 的值是 .
的值是 . 满足
满足 ,记
,记 表示不超过实数x的最大整数,则
表示不超过实数x的最大整数,则



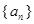 的前
的前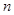 项和
项和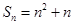
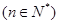 ,则
,则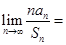 _______.
_______. 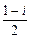 )n,(n∈N*),记Sn=|z2-z1|+|z3-z2|+…+|zn+1-zn|,则
)n,(n∈N*),记Sn=|z2-z1|+|z3-z2|+…+|zn+1-zn|,则 Sn=_________.
Sn=_________.