题目内容
设等差数列{an}的公差不为0,其前n项和是Sn.若S2=S3,Sk=0,则k=______.
∵S2=S3,∴S3-S2=0=a3,∴a1+2d=0,∴a1=-2d≠0.
又Sk=0,则ka1+
d=0,∴2a1+(k-1)d=0.
把a1=-2d≠0.代入上式得-4d+(k-1)d=0,化为-4+k-1=0,解得k=5.
故答案为5.
又Sk=0,则ka1+
| k(k-1) |
| 2 |
把a1=-2d≠0.代入上式得-4d+(k-1)d=0,化为-4+k-1=0,解得k=5.
故答案为5.

练习册系列答案
相关题目
 ,数列{
,数列{ }是公差为d的等差数列,数列{
}是公差为d的等差数列,数列{ }是公比为q的等比数列(q≠1,
}是公比为q的等比数列(q≠1, ),若
),若 ,
,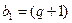 ,
, .
. }的前n项和为
}的前n项和为 ,对
,对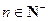 都有
都有 …
… 求
求 .
.