��Ŀ����
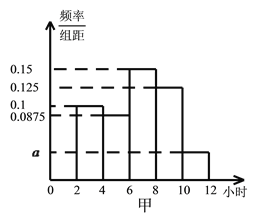
����Ŀ��ijУ�Ը�һ�꼶ѧ�����ٲμ���������Ĵ���������ͳ�ƣ������ȡ��M��ѧ����Ϊ�������õ���M��ѧ���μ���������Ĵ��������ݴ�����������Ƶ�ʷֲ�ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��
���� | Ƶ�� | Ƶ�� |
[10��15�� | 20 | 0.25 |
[15��20�� | 50 | n |
[20��25�� | m | p |
[25��30�� | 4 | 0.05 |
�ϼ� | M | N |
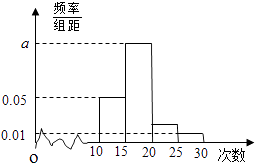
��1�������n��p��ֵ��Ƶ�ʷֲ�ֱ��ͼ��a��ֵ��������Ƶ�ʷֲ�ֱ��ͼ���Ƹ�У��һѧ�����ٲμ����������������λ����
��2������÷ֲ�����ķ������������������[10��15����[25��30�������й���ȡ6�ˣ��ٴ���6����ѡ2�ˣ���2�˷����������[10��15���ĸ��ʣ�
���𰸡�
��1���⣺��20��M=0.25����M=80���� ![]() ��
�� ![]() ��
��
![]() ��
��
��������[15��20�����������15+x����
��0.125x=0.25������x=2������ѧ���μ����������������λ��Ϊ17�Σ�
��2���⣺������֪�������������[10��15����20�ˣ��������������[25��30����4�ˣ�
����÷ֲ�����ķ������������������[10��15����[25��30�������й���ȡ6�ˣ�
���ȡ�ķ��������[10��15����[25��30���������ֱ�Ϊ�� ![]() ��
�� ![]() ��
��
�Ƿ��������[10��15��Ϊa1��a2��a3��a4��a5����[25��30����Ϊb��
���ѳ�ȡ��6������ѡ���˵����п���Ϊ�� ![]()
��15�֣�
�衰2�˷����������[10��15����Ϊ�¼�A�����¼�A������ ![]()
��10�֣�
���� ![]() ��
��
����������1������Ƶ�ʷֲ������M��p��n��ֵ����������λ���Ķ������ѧ���μ����������������λ������2���������ȡ�ķ��������[10��15����[25��30�����������������оٷ���ô��ѳ�ȡ��6������ѡ���˵����п��ܹ���15�֣��ҳ����С�2�˷����������[10��15�������¼�A�ĸ���Ϊ10�֣��Ӷ�����¼�A�ĸ��ʣ�
�����㾫����������Ĺؼ���������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ������Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��

����Ŀ��ijְ�ƽ������������Բμ�ij��רҵ�������Ե�100�˵ijɼ�������ͳ�ƣ�������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�����涨80�ּ������߽����ɹ����������ʧ�ܣ�����Ϊ100�֣���
�����ɹ� | ����ʧ�� | �ϼ� | |
�� | 16 | ||
Ů | 50 | ||
�ϼ� |
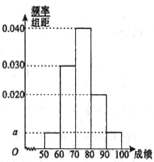
������ͼ��![]() ��ֵ��
��ֵ��
��������֪�����������![]() �����������ж��ܷ���85%�İ�����Ϊ�������ɹ������Ա��йأ�
�����������ж��ܷ���85%�İ�����Ϊ�������ɹ������Ա��йأ�
����Ƶ����Ϊ���ʣ��ӱ��ο��Ե�������Ա�У������ȡ4�˽���Լ̸������4���н���ʧ�ܵ�����Ϊ![]() ����
����![]() �ķֲ�������ѧ����
�ķֲ�������ѧ����![]() ��
��
���ο���ʽ��![]() ������
������![]() ��
��
| 0��40 | 0��25 | 0��15 | 0��10 | 0��05 | 0��025 |
| 0��780 | 1��323 | 2��072 | 2��706 | 3��841 | 5��024 |