��Ŀ����
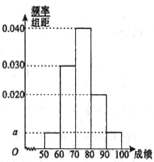
����Ŀ��ijְ�ƽ������������Բμ�ij��רҵ�������Ե�100�˵ijɼ�������ͳ�ƣ�������Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ�����涨80�ּ������߽����ɹ����������ʧ�ܣ�����Ϊ100�֣���
�����ɹ� | ����ʧ�� | �ϼ� | |
�� | 16 | ||
Ů | 50 | ||
�ϼ� |
������ͼ��![]() ��ֵ��
��ֵ��
��������֪�����������![]() �����������ж��ܷ���85%�İ�����Ϊ�������ɹ������Ա��йأ�
�����������ж��ܷ���85%�İ�����Ϊ�������ɹ������Ա��йأ�
����Ƶ����Ϊ���ʣ��ӱ��ο��Ե�������Ա�У������ȡ4�˽���Լ̸������4���н���ʧ�ܵ�����Ϊ![]() ����
����![]() �ķֲ�������ѧ����
�ķֲ�������ѧ����![]() ��
��
���ο���ʽ��![]() ������
������![]() ��
��
| 0��40 | 0��25 | 0��15 | 0��10 | 0��05 | 0��025 |
| 0��780 | 1��323 | 2��072 | 2��706 | 3��841 | 5��024 |
���𰸡���1��![]() ����2���г���85%�İ�����Ϊ�������ɹ������Ա��йأ���3������Ϊ3��
����2���г���85%�İ�����Ϊ�������ɹ������Ա��йأ���3������Ϊ3��
�����������������(��)��Ƶ�ʷֲ�ֱ��ͼ��С����������ܺ�Ϊ![]() ���������
���������![]() ��
��
(��)��Ƶ�ʷֲ�ֱ��ͼ֪�������ɹ���Ƶ��Ϊ![]() ���õ������ɹ�������Ϊ
���õ������ɹ�������Ϊ![]() ���ˣ���
���ˣ���
�õ�![]() �������������ݹ�ʽ���
�������������ݹ�ʽ���![]() ��ֵ�����ɵõ����ۣ�
��ֵ�����ɵõ����ۣ�
������Ƶ�ʷֲ�ֱ��ͼ֪����ʧ�ܵ�Ƶ��Ϊ![]() ���õ���
���õ���![]() ����Ϊ���Ӷ���ֲ���
����Ϊ���Ӷ���ֲ���
���ö���ֲ��ĸ��ʹ�ʽ����ø��ʣ��г��ֲ��У��Ӷ���������ֵ��
���������(��)��Ƶ�ʷֲ�ֱ��ͼ��С����������ܺ�Ϊ1����֪
![]() ����
����![]() .
.
(��)��Ƶ�ʷֲ�ֱ��ͼ֪�������ɹ���Ƶ��Ϊ![]() ��
��
�ʽ����ɹ�������Ϊ![]() ���ˣ���
���ˣ���
���������
�����ɹ� | ����ʧ�� | �ϼ� | |
�� | 16 | 34 | 50 |
Ů | 9 | 41 | 50 |
�ϼ� | 25 | 75 | 100 |
���衰�����ɹ������Ա��أ�
�����ϱ����ݴ��빫ʽ�ɵ�![]() ��
��
�����г���85%�İ�����Ϊ�������ɹ������Ա��йأ�
������Ƶ�ʷֲ�ֱ��ͼ֪����ʧ�ܵ�Ƶ��Ϊ![]() ����Ƶ����Ϊ���ʣ���ӱ��ο��Ե�������Ա�У������ȡ1�˽���Լ̸�����˽���ʧ�ܵĸ���Ϊ
����Ƶ����Ϊ���ʣ���ӱ��ο��Ե�������Ա�У������ȡ1�˽���Լ̸�����˽���ʧ�ܵĸ���Ϊ![]() ��
��
��![]() ����Ϊ���Ӷ���ֲ���
����Ϊ���Ӷ���ֲ���
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
��![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
![]() ��
��![]() .
.