题目内容
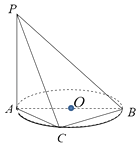
【题目】已知圆锥曲线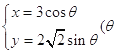 
为参数）和定点 
F1 ， F2是圆锥曲线的左右焦点。
（1）求经过点F2且垂直于直线AF1的直线l的参数方程；
（2）以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，求直线AF2的极坐标方程.
【答案】
（1）解：圆锥曲线
化为普通方程）
所以 ， ，则直线 的斜率
于是经过点 且垂直于直线 的直线l的斜率
直线l的倾斜角为
所以直线l参数方程 ，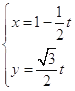 
（2）解：直线AF2的斜率k=- ，倾斜角是120°，设P（ρ，θ）是直线AF2上任一点即ρsin（120°-θ）=sin60°，化简得 ρcosθ+ρsinθ= ，故可知
【解析】本题主要考查了椭圆的参数方程，解决问题的关键是（1）利用三角函数中的平方关系消去参数θ，将圆锥曲线化为普通方程，从而求出其焦点坐标，再利用直线的斜率求得直线L的倾斜角，最后利用直线的参数方程形式，即可得到直线L的参数方程．（2）设P（ρ，θ）是直线AF2上任一点，利用正弦定理列出关于ρ、θ的关系式，化简即得直线AF2的极坐标方程．
【考点精析】本题主要考查了椭圆的参数方程的相关知识点，需要掌握椭圆
的参数方程可表示为
才能正确解答此题．
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计，随机抽取了M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频率分布统计表和频率分布直方图如图：
分组 | 频数 | 频率 |
[10，15） | 20 | 0.25 |
[15，20） | 50 | n |
[20，25） | m | p |
[25，30） | 4 | 0.05 |
合计 | M | N |
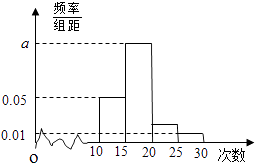
（1）求表中n，p的值和频率分布直方图中a的值，并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数；
（2）如果用分层抽样的方法从样本服务次数在[10，15）和[25，30）的人中共抽取6人，再从这6人中选2人，求2人服务次数都在[10，15）的概率．
