题目内容
【题目】已知函数![]() .
.
(I)当a=2时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(II)设函数![]() ,z.x.x.k讨论
,z.x.x.k讨论![]() 的单调性并判断有无极值,有极值时求出极值.
的单调性并判断有无极值,有极值时求出极值.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析。
;(Ⅱ)见解析。
【解析】试题分析:(Ⅰ)根据导数的几何意义,求出切线的斜率,再用点斜式写出切线方程;(Ⅱ)由![]() ,通过讨论确定
,通过讨论确定![]() 的单调性,再由单调性确定极值.
的单调性,再由单调性确定极值.
试题解析:(Ⅰ)由题意![]() ,
,
所以,当![]() 时,
时, ![]() ,
, ![]() ,
,
所以![]() ,
,
因此,曲线![]() 在点
在点![]() 处的切线方程是
处的切线方程是![]() ,
,
即![]() .
.
(Ⅱ)因为![]() ,
,
所以![]() ,
,
![]()
![]() ,
,
令![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,
,
所以,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
(1)当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增.
单调递增.
所以当![]() 时
时![]() 取到极大值,极大值是
取到极大值,极大值是![]() ,
,
当![]() 时
时![]() 取到极小值,极小值是
取到极小值,极小值是![]() .
.
(2)当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
所以![]() 在
在![]() 上单调递增,
上单调递增, ![]() 无极大值也无极小值.
无极大值也无极小值.
(3)当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() ,
, ![]() 单调递增.
单调递增.
所以当![]() 时
时![]() 取到极大值,极大值是
取到极大值,极大值是![]() ;
;
当![]() 时
时![]() 取到极小值,极小值是
取到极小值,极小值是![]() .
.
综上所述:
当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,函数既有极大值,又有极小值,极大值是
上单调递减,函数既有极大值,又有极小值,极大值是![]() ,极小值是
,极小值是![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
当![]() 时,函数
时,函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,函数既有极大值,又有极小值,极大值是
上单调递减,函数既有极大值,又有极小值,极大值是![]() ,极小值是
,极小值是![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如图:
分组 | 频数 | 频率 |
[10,15) | 20 | 0.25 |
[15,20) | 50 | n |
[20,25) | m | p |
[25,30) | 4 | 0.05 |
合计 | M | N |
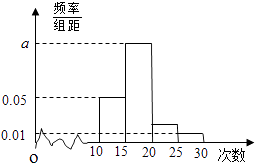
(1)求表中n,p的值和频率分布直方图中a的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
(2)如果用分层抽样的方法从样本服务次数在[10,15)和[25,30)的人中共抽取6人,再从这6人中选2人,求2人服务次数都在[10,15)的概率.