题目内容
【题目】已知曲线 
(t为参数)， 
( 
为参数)．
（1）化 
， 
的方程为普通方程，并说明它们分别表示什么曲线；
（2）过曲线 的左顶点且倾斜角为 
的直线 
交曲线 于 
两点，求 
【答案】
（1）解：
曲线 为圆心是 ，半径是1的圆．
曲线 为中心是坐标原点，焦点在x轴上，长轴长是8，短轴长是6的椭圆．
（2）解：曲线 的左顶点为 ，则直线 
的参数方程为 
（ 为参数）
将其代入曲线 整理可得： ，设 对应参数分别为 ，则
所以 ．
【解析】分析：本题主要考查了椭圆的参数方程，解决问题的关键是（1）根据 
消参.（2）由曲线 
的直角坐标方程可知其左顶点为 
,从而可得直线 的参数方程,将直线 的参数方程代入曲线 
整理可得关于参数 
的一元二次方程,根据韦达定理可得两根之和,两根之积.由 的几何意义可得 
.
【考点精析】利用椭圆的参数方程对题目进行判断即可得到答案，需要熟知椭圆
的参数方程可表示为
．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计，随机抽取了M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频率分布统计表和频率分布直方图如图：
分组 | 频数 | 频率 |
[10，15） | 20 | 0.25 |
[15，20） | 50 | n |
[20，25） | m | p |
[25，30） | 4 | 0.05 |
合计 | M | N |
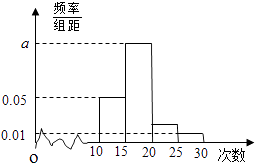
（1）求表中n，p的值和频率分布直方图中a的值，并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数；
（2）如果用分层抽样的方法从样本服务次数在[10，15）和[25，30）的人中共抽取6人，再从这6人中选2人，求2人服务次数都在[10，15）的概率．
