题目内容
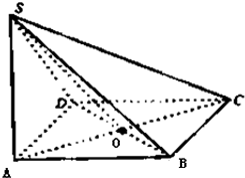
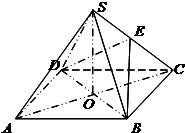
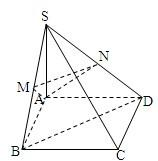
如图,四棱锥S?ABCD中,底面ABCD是正方形,SA⊥面ABCD,且SA=AB,M、N分别为SB、SD中点,求证:
(1)DB∥平面AMN.
(2)SC⊥平面AMN.
(1)DB∥平面AMN.
(2)SC⊥平面AMN.

证:(1)∵M,N分别为SB,SD的中点
∴MN∥BD∵MN?面AMN,BD?面AMN
∴BD∥平面AMN
(2)∵SA⊥平面ABCD,AC⊥BD
∴SC⊥BD∴SC⊥MN
又∵CD⊥AD,SA⊥CD
∴CD⊥平面SAD,∴CD⊥AN,
又AN为等腰直角三角形SAD斜边中线,所以AN⊥SD
∴AN⊥平面SCD∴AN⊥SC
∴SC⊥平面AMN.

∴MN∥BD∵MN?面AMN,BD?面AMN
∴BD∥平面AMN
(2)∵SA⊥平面ABCD,AC⊥BD
∴SC⊥BD∴SC⊥MN
又∵CD⊥AD,SA⊥CD
∴CD⊥平面SAD,∴CD⊥AN,
又AN为等腰直角三角形SAD斜边中线,所以AN⊥SD
∴AN⊥平面SCD∴AN⊥SC
∴SC⊥平面AMN.

练习册系列答案
相关题目