题目内容

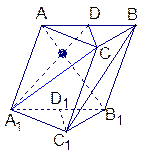
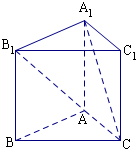
边长为1的正方形ABCD沿对角线BD折起，形成三棱锥C-ABD，它的主视图与俯视图如图所示，则异面直线AB与CD所成角为______．
设折叠前C点的位置为C'，AC、BD的交点为O，则
∵根据三视图，可得平面BCD⊥平面ABD，平面BCD∩平面ABD=BD且CO⊥BD
∴CO⊥平面ABD
∵OC'?平面ABD，∴CO⊥OC'
∵CO=C'O=
2
2
，∴CC'=
OC2+C′O2
=1
∵DC'=DC=1，∴△DCC'是边长为1的等边三角形，可得∠CDC'=60°
∵正方形ABC'D中，AB∥C'D，
∴∠CDC'就是异面直线AB与CD的所成角，
因此，异面直线AB与CD的所成角为60°
故答案为：60°
练习册系列答案
相关题目
已知斜三棱柱ABC—A1B1C1中，A1C1=B1C1=2，D、D1分别是AB、A1B1的中点，平面A1ABB1⊥平面A1B1C1，异面直线AB1和C1B互相垂直.
(1)求证: AB1⊥C1D1；
(2)求证: AB1⊥面A1CD；
(3)若AB1=3，求直线AC与平面A1CD所成的角.
如图∠BAC=90°，等腰直角三角形ABC所在的平面与正方形ABDE所在的平面互相垂直，则异面直线AD与BC所成角的大小是_______．
如图，三棱锥P-ABC中，PA⊥平面ABC，△ABC是等边三角形，E是BC中点，若PA=AB，则异面直线PE与AB所成角的余弦值（　　）
A．
3
7
14
B．
21
6
C．
5
10
D．
2
3
如图，在四棱锥P-ABCD中，已知PA⊥平面ABCD，PB与平面ABC成60°的角，底面ABCD是直角梯形，∠ABC=∠BAD=90°，AB=BC=
1
2
AD．
（1）求证：平面PCD⊥平面PAC；
（2）设E是棱PD上一点，且PE=
1
3
PD，求异面直线AE与PB所成的角．
三棱柱ABC-A1B1C1中，底面边长和侧棱长都相等，∠BAA1=∠CAA1=60°，则异面直线AB1与BC1所成角的余弦值为（　　）
A．
3
3
B．
6
6
C．
3
4
D．
3
6
已知正三棱柱ABC-A1B1C1的底面边长为8，侧棱长为6，D为AC中点．
（1）求证：AB1∥平面C1DB；
（2）求异面直线AB1与BC1所成角的余弦值．
如图，四面体ABCD中，O、E分别是BD、BC的中点，AO⊥平面BCD，CA=CB=CD=BD=2．
（1）求证：面ABD⊥面AOC；
（2）求异面直线AE与CD所成角的大小．
如图，已知正三棱柱ABC-A1B1C1的各条棱长都相等，则异面直线AB1和A1C所成的角的余弦值大小是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网