题目内容
已知斜三棱柱ABC—A1B1C1中,A1C1=B1C1=2,D、D1分别是AB、A1B1的中点,平面A1ABB1⊥平面A1B1C1,异面直线AB1和C1B互相垂直.
(1)求证: AB1⊥C1D1;
(2)求证: AB1⊥面A1CD;
(3)若AB1=3,求直线AC与平面A1CD所成的角.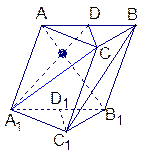
(1)求证: AB1⊥C1D1;
(2)求证: AB1⊥面A1CD;
(3)若AB1=3,求直线AC与平面A1CD所成的角.

(1) 证明略,(2)证明略(3)

(1)证明: ∵A1C1=B1C1,D1是A1B1的中点,
∴C1D1⊥A1B1于D1,
又∵平面A1ABB1⊥平面A1B1C1,
∴C1D1⊥平面A1B1BA,
而AB1 平面A1ABB1,∴AB1⊥C1D1
平面A1ABB1,∴AB1⊥C1D1
(2)证明:连结D1D,
∵D是AB中点,∴DD1 CC1,∴C1D1∥CD,
CC1,∴C1D1∥CD,
由(1)得CD⊥AB1,又∵C1D1⊥平面A1ABB1,C1B⊥AB1,
由三垂线定理得BD1⊥AB1,
又∵A1D∥D1B,∴AB1⊥A1D而CD∩A1D=D,∴AB1⊥平面A1CD
(3)解 由(2)AB1⊥平面A1CD于O,
由(2)AB1⊥平面A1CD于O,
连结CO1得∠ACO为直线AC与平面A1CD所成的角,
∵AB1=3,AC=A1C1=2,∴AO=1,∴sinOCA= ,
,
∴∠OCA= .
.
∴C1D1⊥A1B1于D1,
又∵平面A1ABB1⊥平面A1B1C1,
∴C1D1⊥平面A1B1BA,
而AB1
 平面A1ABB1,∴AB1⊥C1D1
平面A1ABB1,∴AB1⊥C1D1
(2)证明:连结D1D,
∵D是AB中点,∴DD1
 CC1,∴C1D1∥CD,
CC1,∴C1D1∥CD,由(1)得CD⊥AB1,又∵C1D1⊥平面A1ABB1,C1B⊥AB1,
由三垂线定理得BD1⊥AB1,
又∵A1D∥D1B,∴AB1⊥A1D而CD∩A1D=D,∴AB1⊥平面A1CD

(3)解
 由(2)AB1⊥平面A1CD于O,
由(2)AB1⊥平面A1CD于O,连结CO1得∠ACO为直线AC与平面A1CD所成的角,
∵AB1=3,AC=A1C1=2,∴AO=1,∴sinOCA=
 ,
,∴∠OCA=
 .
.
练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为 ,
, ,
, 平面
平面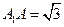 ,
, ,
, ,
, ,
,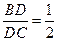 .
. 平面
平面 ;
; 的大小.
的大小.
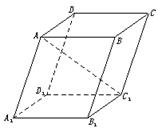
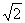 ,则这个棱柱的侧面对角线E1D与BC1所成的角是( )
,则这个棱柱的侧面对角线E1D与BC1所成的角是( ) 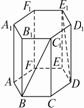
 中,
中, ,则二面角
,则二面角 的平面角的余弦值为( )
的平面角的余弦值为( )




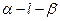 为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.
为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.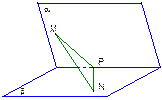


 的平面角为
的平面角为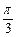 ,AB⊥BC,BC⊥CD,
,AB⊥BC,BC⊥CD, ,BC在l上,
,BC在l上, ,若
,若 ,则AD的长为 .
,则AD的长为 .