题目内容
如图，四面体ABCD中，O、E分别是BD、BC的中点，AO⊥平面BCD，CA=CB=CD=BD=2．
（1）求证：面ABD⊥面AOC；
（2）求异面直线AE与CD所成角的大小．
（1）求证：面ABD⊥面AOC；
（2）求异面直线AE与CD所成角的大小．
（1）∵AO⊥平面BCD，∴AO⊥BD．
∵CB=CD，O是BD的中点，
∴CO⊥BD．
又∵AO∩OC=O，∴BD⊥平面AOC．
∴平面ABD⊥平面AOC．
（2）连接OE，则OE∥CD，
∴∠AEO即为异面直线AE与CD所成角．
在Rt△AOE中，
∵OE=1，AO=1，
∴∠AEO=45°
∴异面直线AE与CD所成角为45°．
∵CB=CD，O是BD的中点，
∴CO⊥BD．
又∵AO∩OC=O，∴BD⊥平面AOC．
∴平面ABD⊥平面AOC．
（2）连接OE，则OE∥CD，
∴∠AEO即为异面直线AE与CD所成角．
在Rt△AOE中，
∵OE=1，AO=1，
∴∠AEO=45°
∴异面直线AE与CD所成角为45°．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
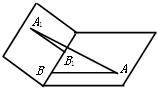
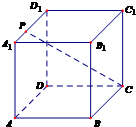
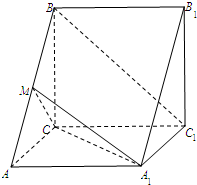
的平面角为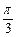
，AB⊥BC，BC⊥CD，
，BC在l上，
，若
，则AD的长为 .