Question

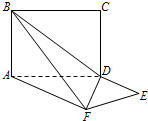
如图，在四棱锥P-ABCD中，已知PA⊥平面ABCD，PB与平面ABC成60°的角，底面ABCD是直角梯形，∠ABC=∠BAD=90°，AB=BC=

1

2

AD．
（1）求证：平面PCD⊥平面PAC；
（2）设E是棱PD上一点，且PE=

1

3

PD，求异面直线AE与PB所成的角．

Answer 1

如图，建立空间直角坐标系A-xyz．
∵PA⊥平面ABCD，PB与平面ABC成60°，
∴∠PBA=60°，∴PA=ABtan60°=

3

．
取AB=1，则A（0，0，0），B（1，0，0），C（1，1，0），P（0，0，

3

），D（0，2，0）．
（1）∵

AC

=（1，1，0），

AP

=（0，0，

3

），

CD

=（-1，1，0），
∴

AC

•

CD

=-1+1+0=0，

AP

•

CD

=0．
∴AC⊥CD，AP⊥CD，
∵AC∩AP=A，
∴CD⊥平面PAC．
又CD?平面PCD，
∴平面PCD⊥平面PAC．
（2）∵

PE

=

1

3

PD

，

PD

=(0，2，-

3

)，
∴

OE

=

OP

+

1

3

PD

=（0，0，

3

）+

1

3

(0，2，-

3

)=(0，

2

3

，

2 3

3

)，
∴E（0，

2

3

，

2 3

3

），∴

AE

=（0，

2

3

，

2 3

3

）．
又

PB

=（1，0，-

3

），∴

AE

•

PB

=-2．
∴cos＜

AE

•

PB

＞=

AE • PB

| AE |•| PB |

=

-2

4 3 ×2

=-

3

4

．
∴异面直线AE与PB所成的角为arccos

3

4

．