题目内容
15.代数式(1-x)(1+x)5的展开式中x3的系数为0.分析 根据二项展开式的通项公式,结合多项式系数的特征,求出结果即可.
解答 解:∵(1-x)(1+x)5=(1-x)(${C}_{5}^{0}$+${C}_{5}^{1}$•x+${C}_{5}^{2}$•x2+${C}_{5}^{3}$•x3+${C}_{5}^{4}$•x4+${C}_{5}^{5}$•x5),
∴(1-x)(1+x)5 展开式中x3的系数为
1×${C}_{5}^{3}$-1×${C}_{5}^{2}$=0.
故答案为:0.
点评 本题考查了二项式定理的应用问题,重点是二项展开式的通项公式,二项式系数的性质,是基础题目.

练习册系列答案
相关题目
7.已知函数f(x)=e2x,g(x)=lnx+$\frac{1}{2}$,对?a∈R,?b∈(0,+∞),使得f(a)=g(b),则b-a的最小值为( )
| A. | $1+\frac{ln2}{2}$ | B. | $1-\frac{ln2}{2}$ | C. | $2\sqrt{e}-1$ | D. | $\sqrt{e}-1$ |
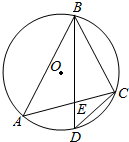 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.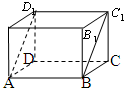 如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114.
如图,在长方体ABCD-A1B1C1D1中,AB=5,BC=4,AA1=3,沿该长方体对角面ABC1D1将其截成两部分,并将它们再拼成一个新的四棱柱,那么这个四棱柱表面积的最大值为114.